Unidade H - Estruturas Algébricas

H.4 Grupos Isomorfos

Definição: Isomorfismo de Grupos: Sejam [S, Δ] e [T, ⌈] grupos. Uma aplicação f:S → T é um isomorfismo de [S, Δ] em [T, ⌈] se

• a função f é bijetora;
• quaisquer que sejam x, y ∈ S, f(x Δ y) = f(x) ⌈ f(y).

A propriedade (2) significa que f é um homomorfismo.

Exemplo H.12: Sejam os grupos [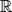⁺, ´] e [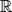, +], x e + as operações de multiplicação e adição, respectivamente, no conjunto dos números reais, b um número real positivo, b ≠ 1, e f a função de 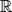⁺ em 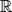definida por

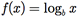
Prove que f é um isomorfismo.

a) Prova: a função f é bijetora
Temos que mostrar que a função f é injetora e sobrejetora.
Vamos mostrar que f é sobrejetora: se r ∈ 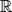, b^r ∈ 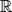⁺ e f(b^r) = log_b b^r = r.
Além disso, f é injetora: se f(x₁) = f(x₂), então logb x₁ = log_b x₂. Seja p = log_b x₁ = log_b x₂. Então, b^p = x₁ e b^p = x₂, logo x₁ = x₂.

b) Prova: f é um homomorfismo
Se x₁, x₂ ∈ 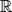⁺, f(x₁ × x₂) = logb (x₁ × x₂) = logb x₁ + logb x₂ = f(x₁) + f(x₂).

Observe que log_b 1 = 0, de modo que f leva 1 (a identidade de [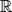⁺, ×]) em 0 (a identidade de [, +]).

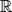Observe também que

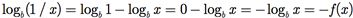
De modo que f leva a inversa de x em [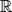, +] na inversa de f(x) em [⁺, ×].

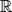Finalmente, ambos os grupos são comutativos.

Assim, os dois grupos do Exemplo H.12 são isomorfos, portanto eles são essencialmente iguais e cada um deles pode ser usado para simular cálculos no outro.

Por exemplo, seja b = 2. Então, [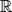, +] pode ser usado para simular o cálculo 64 × 512 em [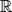⁺, ×]. Primeiro, levemos 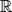⁺ em 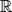através da função f:

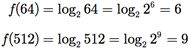
Agora, em [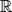, +], efetue o cálculo

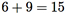
E, finalmente, usamos f−1 para retornar a ⁺: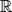

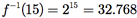
Observação: antigamente, quando não existiam as calculadoras eletrônicas, números muito grandes eram multiplicados usando-se tabelas de logaritmos com base 10, tal que se convertia um problema de multiplicação em um de adição.

Exemplo H.13: Considere o grupo [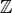, +] e a função f(x) = 0.

A função f é um homomorfismo do grupo [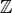, +] no grupo [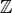, +], pois f(x + y) = 0 = 0 + 0 = f(x) + f(y). No entanto, f não é uma função bijetora, portanto não é um isomorfismo.

Exemplo H.14: Considere o grupo [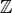, +] e a função h(x) = x + 1.

A função h é uma função bijetora, pois h(x) = h(y) implica em que x + 1 = y + 1, ou seja, x = y, logo h é injetora; h também é sobrejetora porque, qualquer que seja z ∈ 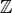, z − 1 ∈ 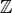e h(z − 1) = z.

Porém, h não é um homomorfismo do grupo [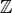, +] no grupo [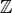, +], pois h(x + y) = x + y + 1 ≠ (x + 1) + (y + 1) = h(x) + h(y). Portanto, h não é um isomorfismo.