I.1 Estrutura da Álgebra de Boole
Modelos e Generalizações
Um exemplo notável de estrutura algébrica é a álgebra booleana ou Álgebra de Boole (George Boole), formulada inicialmente para modelar a lógica proposicional e utilizada posteriormente por Shannon (1938) para modelar circuitos eletrônicos (ou digitais).
O ponto de partida para o projeto sistemático de sistemas de processamento digital é a chamada Álgebra de Boole, trabalho de um matemático inglês que, em um livro de 1854, propõe dar expressão às leis fundamentais do raciocínio na linguagem simbólica do cálculo. Trata-se, portanto, de uma formalização matemática da lógica em sua forma mais simples, conhecida como Lógica Proposicional.
Essa lógica permite tratar da interpretação (isto é, atribuição de valor verdadeiro ou falso) de proposições isoladas, ou da combinação de proposições por meio de operações lógicas simples.
A proposta original de Boole estava mais próxima do que hoje se chama álgebra elementar, isto é, trabalhava com operações usuais, como soma e multiplicação, interpretando as expressões resultantes em termos de lógica. Por exemplo, ao identificar a multiplicação de duas variáveis x e y como uma expressão lógica de objetos que contêm ao mesmo tempo as propriedades representadas por x e por y, ele chega à necessidade da expressão x × x = x, e daí à ideia de que só dois valores seriam válidos neste cálculo, 0 e 1.
Já o significado moderno de álgebra (ou estrutura algébrica) é bem mais abstrato, e de apresentação mais complexa. No que se segue, veremos os principais resultados deste cálculo para embasar a teoria da simplificação de operações lógicas.
Assim, a álgebra de Boole é, simplesmente, um modelo ou generalização para tratarmos com proposições lógicas que podem ser falsas ou verdadeiras, investigando-as através dos operadores booleanos (operadores lógicos).
Definição e Propriedades
Definição: Álgebra de Boole: Uma álgebra de Boole é um conjunto A no qual estão definidas duas operações binárias, + e × , e uma operação unária, ′, e que contém dois elementos distintos, 0 e 1, tais que as seguintes propriedades são válidas, quaisquer que sejam x, y, z ∈ A:
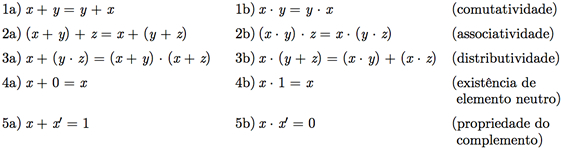
A partir de agora, vamos denotar uma álgebra de Boole por [A, +, ⋅, ′, 0, 1].
Considere o conjunto A = {0, 1} e defina operações binárias + e × em A por x + y = max(x, y) e x × y = min(x, y). Essas operações binárias podem ser ilustradas pelas tabelas I.1 e I.2.
A operação unária ′é descrita pela Tabela I.3.
Tabela I.3 Operação unária ′.
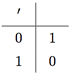
Assim, 0′ = 1 e 1′ = 0. Então, [A, +, ×, ′, 0, 1] é uma álgebra de Boole. Podemos provar as 10 propriedades da definição, verificando todos os casos possíveis. Por exemplo, para a propriedade 2a (a associatividade de +), temos que
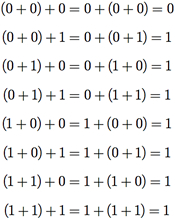
Para a propriedade 4b, temos que
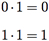
Existem muitas outras propriedades que são válidas em qualquer álgebra de Boole. Essas propriedades adicionais podem ser provadas usando as propriedades dadas na definição.
A idempotência da soma x + x = x é válida, pois
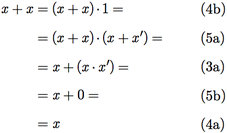
Uma vez demonstrada uma propriedade na álgebra de Boole, essa pode ser usada para demonstrar outras. Na álgebra de Boole, sempre que quisermos realizar uma demonstração do tipo
alguma expressão = alguma outra expressão
podemos nos basear nas sugestões a seguir.
a)Em geral, a melhor abordagem é começar com a expressão mais complexa e tentar provar que ela se reduz à expressão mais simples.
b)Considere somar 0 em alguma forma (como x × x′) ou multiplicar por 1 em alguma forma (como x + x′).
c)Sempre se recorde da propriedade 3a, a distributividade da multiplicação em relação à soma.
d)Recorde-se da idempotência da soma e da multiplicação, x + x = x e x × x = x.
Se x é um elemento de uma álgebra de Boole, o elemento x′ é chamado de complemento de x. O complemento de x satisfaz que
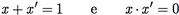
então, x1 = x′.
Prova :
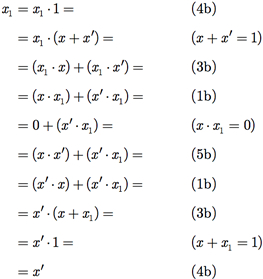
Álgebra de Boole Isomorfa
Duas estruturas são isomorfas se existe uma bijeção (chamada de isomorfismo) que leva elementos de uma estrutura em elementos da outra de modo que as propriedades relevantes são preservadas. Se duas estruturas são isomorfas, cada uma delas é uma imagem espelhada da outra, com os elementos simplesmente renomeados. As duas estruturas são, essencialmente, iguais.
Suponha uma estrutura como a álgebra de Boole com operações binárias e unárias definidas em um conjunto. Então, as propriedades relevantes são como essas operações agem. Um isomorfismo tem que preservar a ação dessas operações. Cada estrutura isomorfa tem que ser idêntica no sentido de que se efetuarmos a operação e, depois, aplicarmos a função obteremos o mesmo resultado que se aplicarmos, primeiro, a função e, depois, efetuarmos a operação. A Figura I.1 ilustra essa ideia.
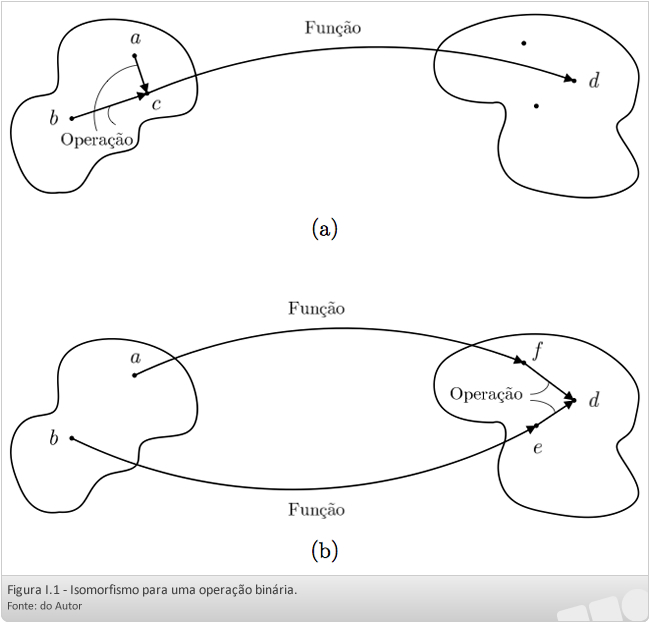
Na Figura I.1(a), efetuamos, primeiro, a operação binária nos elementos a e b, resultando em c e, depois, c é levado em d pela função. Na Figura I.1(b), primeiro aplicamos a função em a e b, obtendo e e f, e, depois, efetuamos a operação binária em e e f, obtendo d, o mesmo elemento que anteriormente. Assim, não esqueçamos que
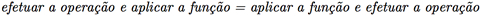
Definição: Isomorfismo entre Álgebras de Boole: Sejam [A, +, ×, ′, 0, 1] e [a, &, ×, ″, α, β] álgebras de Boole. Uma função f:A → a é um isomorfismo de [A, +, ×, ′, 0, 1] em [a, &, ×, ″, α, β] se:
a) f é uma bijeção
b) f(x + y) = f(x) & f(y)
c) f(x × y) = f(x) * f(y)
d) f(x′) = (f(x))″
Teorema sobre Álgebras de Boole Finitas: Seja A uma álgebra de Boole arbitrária com n elementos. Então, n = 2m para algum m e A é isomorfa a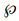 
({1, 2, ..., m}).
O teorema acima nos fornece as informações a seguir.
a)O número de elementos em uma álgebra de Boole é uma potência de 2.
b) As álgebras de Boole formadas pelo conjunto das partes de um conjunto são os únicos tipos de álgebras de Boole finitas que existem.