Unidade I - Álgebra de Boole e Lógica Computacional

I.2 Circuitos Lógicos

Elementos Básicos de Lógica

Em 1938, o matemático americano Claude Shannon percebeu a semelhança entre a lógica proposicional e a lógica de circuitos elétricos e compreendeu que álgebras de Boole poderiam ser utilizadas na interpretação desses circuitos.

Imaginemos que as voltagens em um circuito elétrico sejam de dois tipos: alta e baixa, que representaremos, respectivamente, por 1 e 0. Consideremos também a existência de interruptores no circuito de modo que um sinal igual a 1 fecha o interruptor e um sinal igual a 0 abre o interruptor (observe a Figura I.2).

Agora, vamos fazer a combinação de dois desses interruptores, controlados por x1 e x2, em paralelo. A Figura I.3 apresenta os diversos casos possíveis.

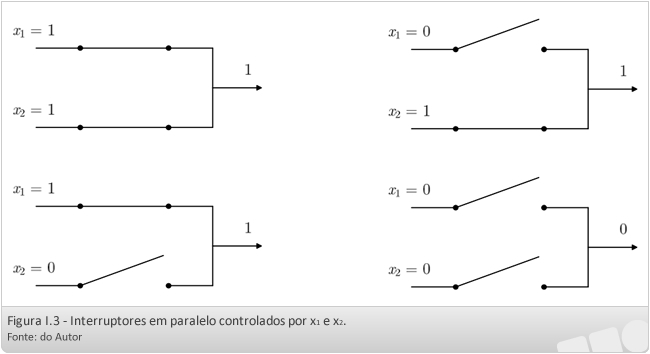
Na figura I.3, observamos que valores de x1 = 0 e x2 = 0 fazem com que os dois interruptores estejam abertos, interrompendo o circuito, de modo que o nível de voltagem na saída é 0. Se um dos valores de x for 1, no entanto, um dos interruptores, ou os dois, estará fechado, resultando em uma saída 1.

A Tabela I.4 resume o comportamento do circuito.

Tabela I.4 Comportamento do circuito com dois disjuntores em paralelo.

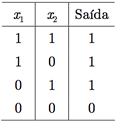
Na Tabela I.4, se nós substituirmos 1 por V e 0 por F, obtemos a tabela-verdade para o conectivo lógico da disjunção. De uma forma mais geral, nós podemos considerar o circuito como sendo um dispositivo eletrônico que implementa a operação booleana +. Outros dispositivos implementam as operações booleanas × e ′. Por exemplo, para a implementação do operador × seriam necessários dois interruptores associados em série, onde ambos devem estar fechados (x1 = 1 e x2 = 1) para se obter uma saída igual a 1.

Os dispositivos mencionados sofreram uma evolução tecnológica, passando de interruptores mecânicos para válvulas eletrônicas, depois transistores, chegando a circuitos integrados.

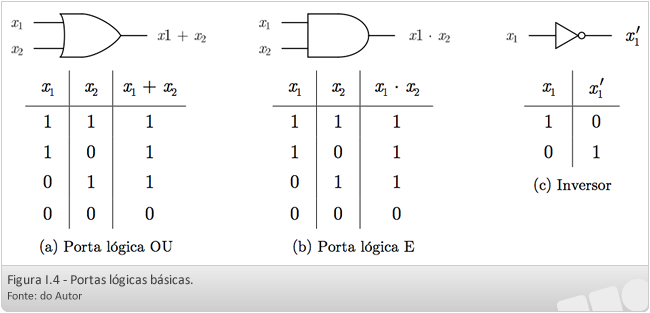
A porta lógica OU, Figura I.4(a), se comporta como a operação booleana +. A porta lógica E, Figura I.4(b), representa a operação booleana ×. A Figura I.4(c) mostra um inversor (negação), que corresponde à operação booleana unária ′. Devido à associatividade das operações + e ×, as portas lógicas OU e E podem ter mais de duas entradas.

Expressões Booleanas

Definição:

Expressão Booleana: Uma expressão booleana em n variáveis x1, x2, ..., xn é qualquer cadeia finita de símbolos formados aplicando-se as seguintes regras:

  1. x1, x2, ..., xn são expressões booleanas.
  2. Se R e S são expressões booleanas, então (R + S), (R × S) e (R)′também o são.

Por convenção, o operador lógico × possui precedência sobre o operador + e o operador ′ tem precedência sobre os operadores + e ×, de modo que x1 + x2 × x3 equivale a x1 + (x2 × x3).

 

Funções Booleanas

Definição: Função Booleana: Uma função booleana é uma função f tal que f:{0, 1}n → {0, 1} para algum inteiro n ≥ 1. A notação {0, 1}n representa o conjunto de todas as n-uplas formadas por 0 e 1. Uma função booleana, portanto, associa um valor 0 ou 1 a cada uma dessas n-uplas.

Exemplo I.1: A tabela-verdade para a operação booleana + descreve uma função booleana f com n = 2. O domínio de f é {(1, 1), (1, 0), (0, 1), (0, 0)} e f(1, 1) = 1, f(1, 0) = 1, f(0, 1) = 1 e f(0, 0) = 0. De forma semelhante, a operação booleana × também descreve uma função booleana com n = 2 e a operação booleana ¢ descreve uma função booleana com n = 1.

Qualquer expressão booleana define uma única função booleana. Veja o exemplo a seguir:

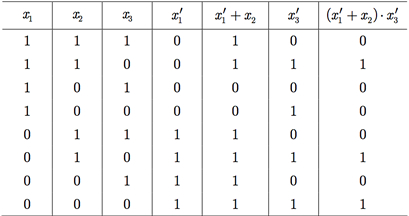
Exemplo I.2: A expressão booleana x1 × x2′ +x3 define a função booleana dada na tabela-verdade da Tabela I.5.

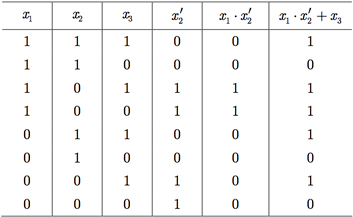
Tabela I.5 Tabela-verdade para a expressão booleana x1 × x2′ +x3

Circuitos e Expressões

Combinando as portas lógicas E, OU e inversores, podemos construir um circuito lógico que representa uma expressão booleana dada e produz a mesma função booleana que a expressão

Exemplo I.3: O circuito lógico para a expressão booleana do Exemplo I.2 está apresentado na Figura I.5.

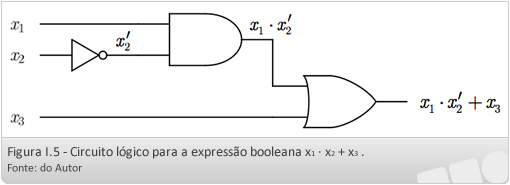
Exemplo I.4: Desenhe os circuitos lógicos para as expressões booleanas:

a) x1 + x2 ′

b) x1 × (x2 + x3)′

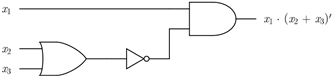
Reciprocamente, se tivermos um circuito lógico, podemos construir uma expressão booleana que possua a mesma função booleana.

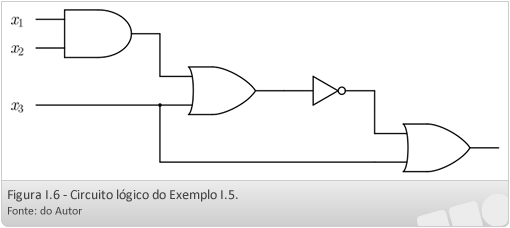
Exemplo I.5: A expressão booleana para o circuito lógico da Figura I.6 é

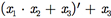
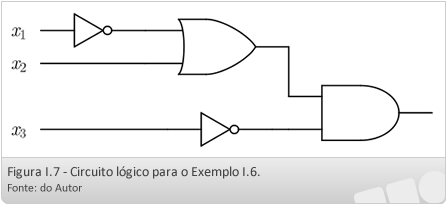
Exemplo I.6: Escreva uma função booleana para o circuito lógico da Figura I.7.

A função booleana para o circuito lógico da Figura I.6 é (x1′ + x2) × x3 ′

Exemplo I.7: Escreva a função booleana em forma de tabela-verdade para o circuito lógico do Exemplo I.6.

Circuitos lógicos construídos com portas lógicas E, OU e inversores são conhecidos como circuitos combinatórios. Podemos resumir as características desses circuitos como:

  1. As linhas de entrada e saída estão ligadas apenas por portas lógicas.
  2. As linhas podem se separar para servir de entrada a mais de uma porta lógica.
  3. Não existem circuitos de realimentação, isto é, a saída de uma porta lógica nunca pode servir de entrada para essa mesma porta.
  4. A saída de um circuito é uma função instantânea das entradas, ou seja, qualquer alteração que ocorra em, pelo menos, uma das entradas, implicará em imediata alteração da saída do circuito.

Formas Normais

Até o momento, o nosso conhecimento de lógica combinacional nos permite:

Agora, estaremos interessados em obter uma expressão booleana (e, portanto, um circuito lógico) a partir de uma função booleana.

Suponha que queiramos determinar uma expressão booleana para a função booleana f dada na Tabela I.6.

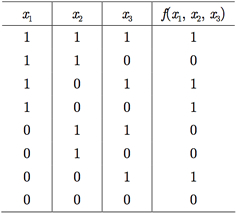
A tabela-verdade possui quatro linhas onde f é igual a 1 (linhas 1, 3, 4 e 7). A forma básica de nossa expressão vai ser uma soma de quatro termos, ( ) + ( ) + ( ) + ( ), de modo que o primeiro termo somente é 1 para os valores da linha 1 e para nenhum outro valor. O segundo termo somente é 1 para os valores da linha 3 e para nenhum outro valor; e assim por diante. Dessa forma, a expressão toda é igual a 1 para os valores indicados das variáveis e para nenhum outro valor (isso é exatamente o que queremos). Quaisquer outros valores nas variáveis de entrada tornarão cada termo nulo e isso implicará saída também nula.

Cada termo na soma será do tipo α × β × γ, onde α é x1 ou x1′, b é x2 ou x2′ e γ é x3 ou x3′. Se o valor de xi, i = 1, 2, 3, na linha em que o valor da função é 1 for 1, usamos o próprio xi; caso o valor de xi nessa linha seja 0, nós usamos xi′. Esses valores irão fazer com que o termo α × β × γ seja 1 para essa linha e 0 para todas as outras. Assim, temos

Portanto, a expressão final é

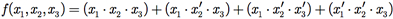
O procedimento descrito, sempre nos conduzirá a uma expressão para a função que é uma soma de produtos, conhecida como forma normal disjuntiva ou forma canônica em soma de produtos para a função booleana.

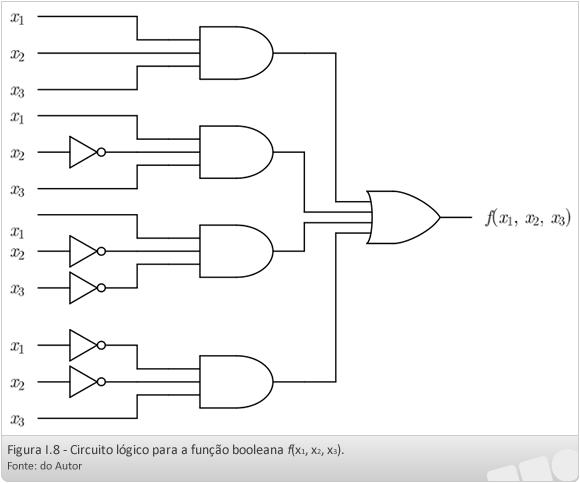
Como qualquer expressão booleana possui um circuito lógico correspondente, qualquer função booleana possui um circuito lógico que a implementa. A Figura I.8 mostra o circuito lógico associado à forma normal disjuntiva da função booleana f(x1, x2, x3).

Exemplo I.8: Considere a tabela-verdade da Tabela I.7.

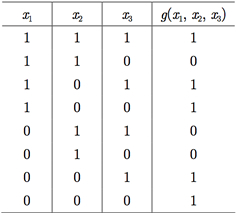
a)Determine a forma normal disjuntiva para a função booleana g(x1, x2, x3).

Observemos que as linhas que possuem o valor 1 para a função g e as suas respectivas entradas na forma α × β × γ são:

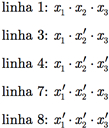
Então, podemos escrever a expressão booleana para a função g(x1, x2, x3) como

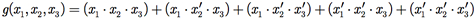
b)Construa o circuito lógico que a implemente.

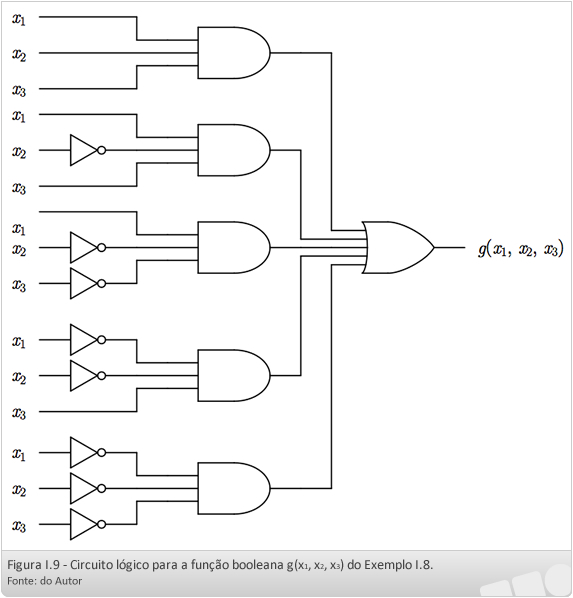
A Figura I.9 mostra o circuito lógico que implementa a função booleana g.

Minimização

Uma determinada função booleana pode ser representada por mais de uma expressão booleana e, portanto, por mais de um circuito lógico composto por portas lógicas E, OU e inversores.

Definição: Expressões Booleanas Equivalentes: Duas expressões booleanas são equivalentes se correspondem às mesmas funções lógicas.

Quando estamos pensando em implementar um circuito lógico associado a uma função booleana, queremos encontrar o circuito mais simples possível (com a menor quantidade de portas lógicas). Para reduzir uma expressão booleana a outra equivalente mais simples, nós podemos usar as propriedades da álgebra de Boole, visto que elas expressam equivalência de expressões booleanas. Por exemplo, se X é uma expressão booleana contendo um termo do tipo x1 + x2 × x3 e Y é a expressão obtida de X substituindo x1 + x2 × x3 pela expressão equivalente (x1 + x2)×(x1 + x3), então X e Y são equivalentes.

Exemplo I.9: Anteriormente, nós determinamos a forma normal disjuntiva para a função booleana f dada pela Tabela I.6. Reduza a expressão de f a uma forma mais simples.

A forma normal disjuntiva encontrada foi

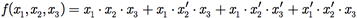
Usando as propriedades da álgebra de Boole, podemos reduzir f(x1, x2, x3) da seguinte forma:

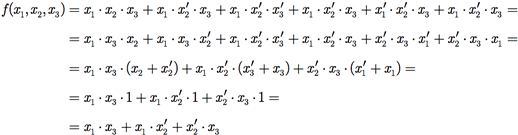
As propriedades da álgebra de Boole utilizadas foram, de acordo com a Seção I.1.2:

Assim, a função f(x1, x2, x3) pode ser implementada mais simplesmente pelo circuito lógico mostrado na Figura I.10.

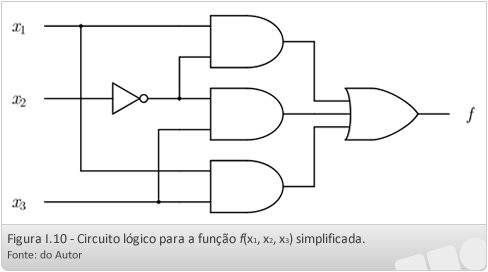
Para percebermos, de uma forma mais clara, a simplificação realizada, compare as Figuras I.8 (circuito original) e Figura I.10 (circuito simplificado).

Exemplo I.10: Simplifique a função g(x1, x2, x3) do Exemplo I.8.

No Exemplo I.8, encontramos a forma normal disjuntiva da função g(x1, x2, x3) como

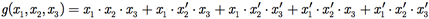
a qual pode ser reduzida como mostrado a seguir.

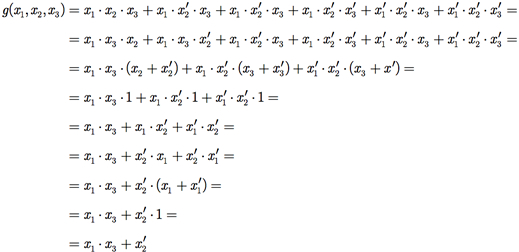
As propriedades booleanas utilizadas na simplificação foram, sequencialmente:

A implementação da função g(x1, x2, x3) simplificada está mostrada na Figura I.11.

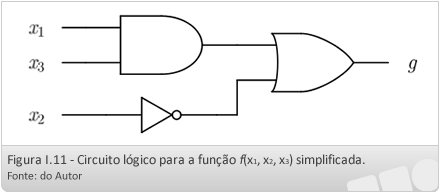
Para uma visualização e compreensão mais claras, compare as Figuras I.9 e I.11.

Caro aluno, conforme vimos nos Exemplos I.9 e I.10, é possível minimizar uma função booleana com a utilização das propriedades da álgebra de Boole. Porém, observe que, para isso, é necessário uma certa dose de criatividade por parte do projetista de circuitos lógicos. Isso faz com que essa forma de minimização não seja frequentemente utilizada. Na sequência dos seus estudos no Curso, você aprenderá uma forma bem mais eficiente de se realizar minimizações em funções booleanas, conhecida como mapas de Karnaugh.

Arranjos Lógicos Programáveis

Um projetista de circuitos integrados, muitas vezes, prefere ao invés de projetar um chip específico para implementar uma determinada função booleana, utilizar um ALP (arranjo lógico programável ou, do inglês, PLA – programmable logic array). Um ALP é um chip que já possui em sua estrutura um arranjo de portas lógicas E e OU, junto com um reticulado retangular de fiação e algumas funções inversoras. Uma vez definida a função booleana em forma normal disjuntiva, interliga-se os componentes necessários do ALP.

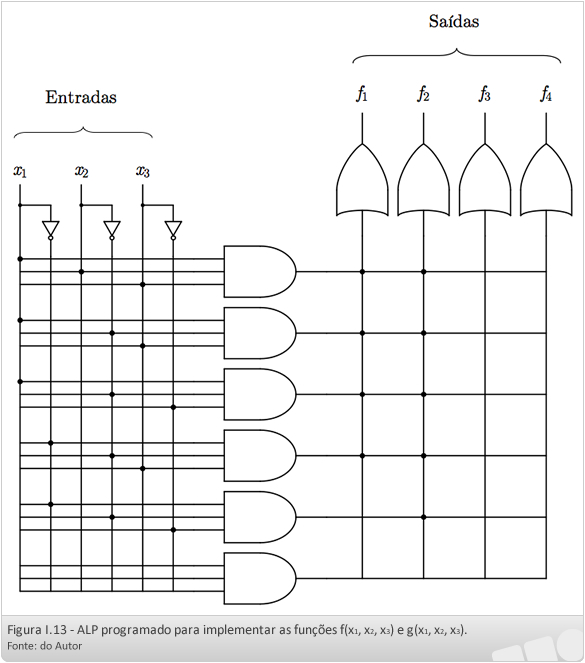
A Figura I.12 ilustra um ALP para três entradas x1, x2 e x3.

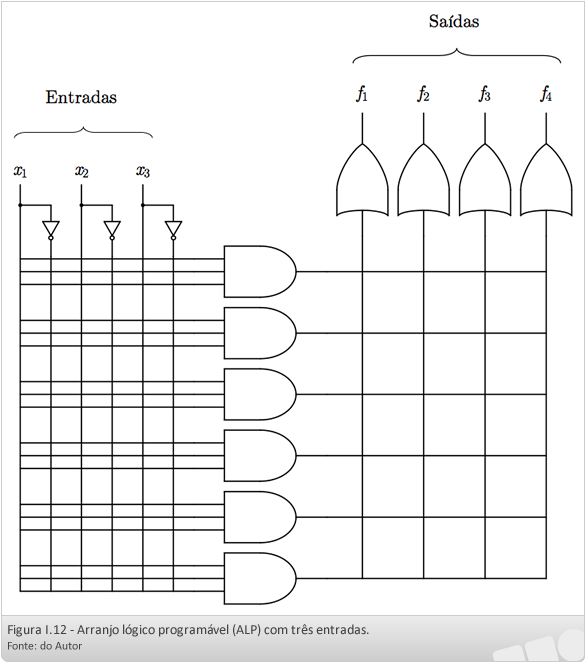
No ALP da figura I.12, observe a existência de quatro linhas de saída, portanto, é possível a implementação de até quatro funções booleanas nesse ALP. Ao se programar o ALP, as linhas horizontais entrando em uma porta E selecionam algumas das variáveis de entrada e, assim, a porta E forma o produto entre essas variáveis. Por outro lado, as linhas verticais que entram em uma porta OU selecionam, quando programadas – conectadas, as saídas das portas E realizando, assim, a soma dessas saídas e resultando na função booleana desejada.

A Figura I.13 mostra como fica a programação do ALP da Figura I.12 para as funções booleanas f(x1, x2, x3) e g(x1, x2, x3) discutidas anteriormente. A função booleana f corresponde à saída f1 e a função g, a saída f2.