Representaçao Numérica
Outra forma de representação de uma variável aleatória é feita através de valores numéricos que quantificam as características marcantes da forma de sua distribuição de frequência.
Tendência central
Essa característica está relacionada com a parte central do histograma de frequências. Em alguns casos existe uma tendência de que o número de ocorrências seja maior na parte central, significando que a variável aleatória costuma ocorrer com maior frequência nos intervalos centrais.
Os parâmetros aqui estudados serão:
- Média aritmética:
- Moda: É o valor representativo do intervalo de classe em que a frequência de ocorrência é máxima, representado no centro do intervalo de classe com maior frequência, pela notação mo.
- Mediana: É o valor que é superado (e não superado) por 50% das ocorrências. Em um histograma de frequências, seria o valor que determinaria áreas iguais à direita e à esquerda, representada pela notação md.
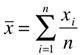
Onde: xi, i=1,2,3,...,n são realizações da variável aleatória, e n o número total de ocorrências, ou seja, o tamanho da amostra.
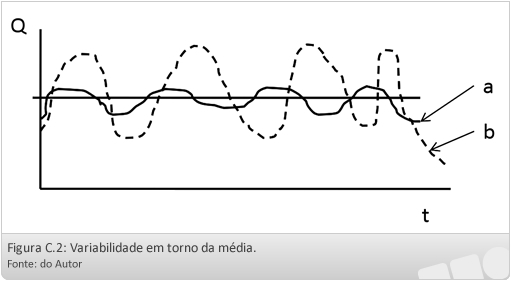
Variabilidade em torno da média
Na figura 16 tem-se a representação de duas séries de vazões fluviais hipotéticas médias mensais, com a média idêntica e a variabilidade em torno da média distinta. Caso fosse pretendida a construção de um reservatório de regularização, o local com histograma b exigiria maior capacidade para armazenar as discrepâncias positivas, que seriam utilizadas para atender às discrepâncias negativas, ou seja, armazenar as cheias para atenuar as estiagens.
Esse exemplo mostra a importância de se contar com um parâmetro numérico para medir a variabilidade.
São eles o desvio padrão e a variância.
- Variância: é a medida de dispersão mais utilizada, seja pela sua facilidade de compreensão e cálculo, seja pela possibilidade de emprego de inferência estatística. A variância é definida como sendo a média dos quadrados dos desvios em relação à média aritmética.
- Desvio padrão: É a raiz quadrada da variância, verifica-se que quanto maior for o desvio padrão ou variância, maior é a flutuação da variável em torno da média.
- Coeficiente de variação: é a medida mais utilizada quando existe interesse em comparar variabilidades de diferentes conjuntos de dados. Embora esta comparação possa ser feita através de outras medidas de variação, nas situações em que as medidas dos conjuntos comparados são muito desiguais ou as unidades de medida são diferentes, devemos utilizar o coeficiente de variação.
- Assimetria: uma distribuição simétrica é aquela que apresenta simetria em relação a um eixo vertical que passa pelo valor modal, ou seja, o valor com maior frequência. Nessa situação a média, a mediana e a moda são iguais. Dentre as várias medidas de assimetria que devem informar se a maioria dos valores se localiza à esquerda ou à direita, ou se estão uniformemente distribuídos em torno da média aritmética é o coeficiente de assimetria denotado por a3. Essa medida indica o grau e a direção do afastamento da simetria e é obtida utilizando o segundo e o terceiro momentos centrados na média, através da seguinte expressão:
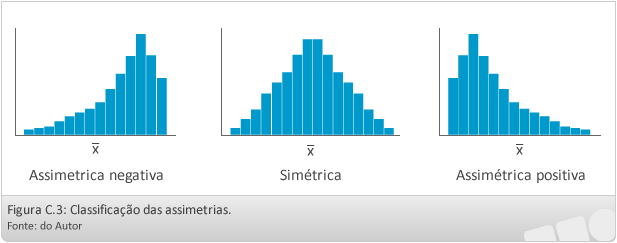
- Se a3 < 0, a distribuição é classificada como assimétrica negativa, indicando que a maioria dos valores são menores ou se localizam à esquerda da média aritmética.
- Se a3 = 0, a distribuição é classificada como simétrica, indicando que os valores estão uniformemente distribuídos em torno da média aritmética.
- Se a3 > 0, a distribuição é classificada como assimétrica positiva, indicando que a maioria dos valores são maiores ou se localizam à direita da média aritmética.
- Momentos: denotados por mn, são medidas calculadas com o propósito de estudar a distribuição. De um modo geral, tanto mais conhecemos uma distribuição quanto mais conhecemos sobre seus momentos. O momento de ordem r centrado num valor a é dado por:
- Quando a = 0, temos os momentos centrados na origem, denominados momentos ordinários de ordem r e representados por m’r.
- Quando a =, temos os momentos de ordem r centrados na média e representados por mr.
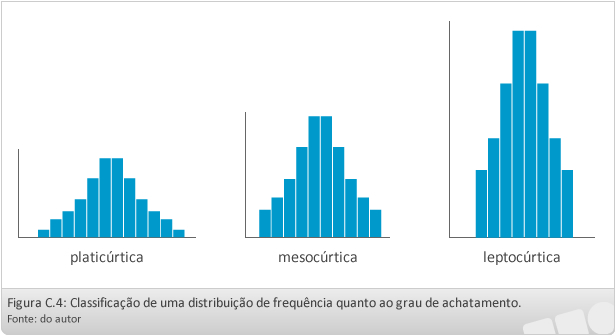
- Curtose: indicam o grau de achatamento de uma distribuição. O coeficiente de curtose denotado por a4, é calculado a partir do segundo momento e do quarto momento centrados na média através da seguinte expressão:
- Se a4 < 3, a distribuição é classificada como platicúrtica, indicando maior achatamento.
- Se a4 = 3, a distribuição é classificada como mesocúrtica, indicando achatamento médio.
- Se a4 > 3, a distribuição é classificada como leptocúrtica, indicando menor achatamento.
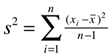
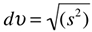
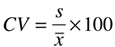
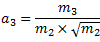
A classificação da distribuição quanto à simetria é feita de acordo com o valor do a3:
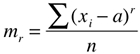
Dois valores de a geram momentos importantes num conjunto de dados:
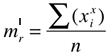
Exemplo:
Para r = 1, temos ![]() ;
;
Para r = 2, temos ![]() ;;
;;
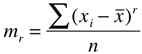
Exemplos:
Para r = 1, temos ![]() ;
;
Para r = 2, teremos ![]() ;
;
Para r = 3, teremos ![]() ;
;
Para r = 4, teremos ![]()
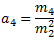
A classificação da distribuição quanto ao grau de achatamento é feita de acordo com o valor de a4: