Capacidade de infiltração e taxa de infiltração

Infiltração acumulada

É a quantidade de água total infiltrada durante determinado tempo. Se quisermos saber a lâmina infiltrada no solo num determinado tempo, basta que se utilize o recurso gráfico, dos quais este é obtido através de ensaios de campo.

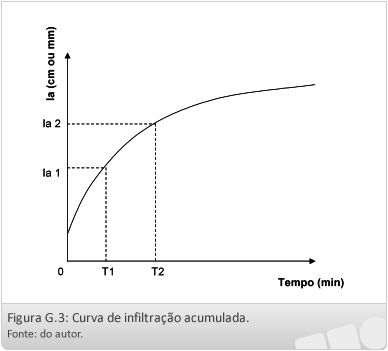
Se desejarmos aplicar uma lâmina de água sobre a superfície do solo, basta utilizarmos o recurso gráfico para determinar o tempo necessária para a aplicação desta lâmina.

Equacionamento geral da infiltração

a) Velocidade ou taxa de infiltração de água no solo

É a razão entre a lâmina de água que infiltra no solo na unidade de tempo. Em função deste conceito obtemos mais três conceitos necessários para o estudo de velocidade de infiltração de água no solo:

- Velocidade de Infiltração Média (VIm);

- Velocidade de Infiltração Aproximada (VIa);

- Velocidade de Infiltração instantânea (VInst).

Velocidade de Infiltração Média (VIm):
É a infiltração acumulada (Ia) em um tempo Ta, dividida pelo próprio tempo acumulado.
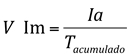
Velocidade de Infiltração Aproximada (VIa):
É o incremento de infiltração DI no intervalo de tempo Dt.
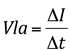
Velocidade de infiltração instantânea (VInst):
É dada pela derivada da infiltração acumulada (Ia) em relação ao tempo (t). É a lâmina (volume de água por unidade de área) que atravessa a superfície do solo por unidade de tempo.

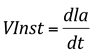
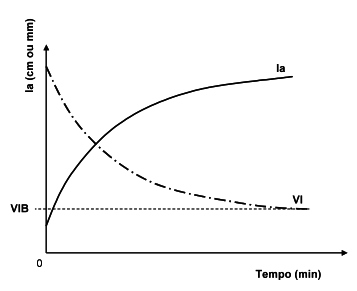
Uma característica muito importante é que independente do tipo de solo a Velocidade de Infiltração (VI) diminui a medida que aumenta o tempo de aplicação de água.

- Inicialmente a VI é alta;

- Com o tempo diminui gradativamente até um valor quase que constante.

No ponto onde a VI apresenta pouca variação, ou seja, seu valor na determinação é quase constante, recebe o nome de Velocidade de Infiltração Básica (VIB).

Assim como na infiltração a VI depende diretamente das característica do solo (textura, estrutura, condutividade hidráulica, camadas impermeáveis, cobertura vegetal, preparo, etc.).

O tempo que o solo levará para atingir a VIB é dependente do tipo de solo em que esta sendo realizada a determinação, como pode ser observado na figura abaixo:

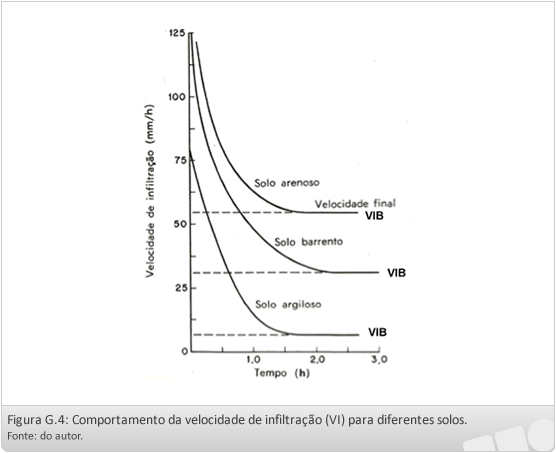
Na literatura é referido que a VIB é praticamente igual ao valor da condutividade hidráulica do solo saturado.

- Considerando o mesmo tipo de solo a VI pode variar dependendo:

Umidade do solo na época de irrigação – quanto maior a umidade menor a VI;

Porosidade – maior quantidade de macroporos maior a VI.

Classificação do solo quanto a VI:

Tipo de solo	VIB (cm/h)
Solo de VIB muito alta	> 3,0
Solo de VIB alta	1,5 – 3,0
Solo de VIB média	0,5 – 1,5
Solo de VIB baixa	< 0,5

b) Determinação da infiltração (I) e Velocidade de Infiltração (VI) de água no solo

- Métodos de campo;

- Modelos de infiltração.

Método de Campo:

Existem vários métodos e maneiras para se determinar a Infiltração e a Velocidade de infiltração de água no solo.

Para que os valores de I e VI sejam significativos, o método escolhido de determinação deve ser condizente com o tipo de estudo que está sendo realizado:

Em função da infiltração e da velocidade de infiltração temos o método do infiltrômetro de anel.

A Velocidade de Infiltração (VI) é a velocidade com que a água penetra no solo através de sua superfície. Basicamente, a velocidade de infiltração depende de certas características do solo, como textura e estrutura, podendo sofrer influência de outros fatores.

A velocidade de infiltração diminui com o tempo, aproximando-se, em geral, de um valor constante que, em certas argilas pesadas, pode chegar a zero, quando atinge estes valores constantes, a velocidade de infiltração passa a se chamar de Velocidade de Infiltração Básica (VIB), que tem grande utilidade nos cálculos de volumes de água.

A VIB esta relacionada diretamente com o tamanho de poro, existente no solo e o tipo de solo, ou seja, a textura do solo é a propriedade que tem maior interferência nesta determinação. Solos com textura mais argilosa possuem poros menores que solos arenosos, em função disso, sua força de adesão (força de ligação da partícula de solo com a partícula de água) é bem maior, em conseqüência, sua a velocidade de infiltração será menor, ou seja a infiltração da água no solo é mais lenta do que solos arenosos.

O total de água infiltrada no solo chamada de Infiltração Acumulada (Ia) fornece o valor total de água infiltrada no solo em forma de lâmina, ao longo do tempo, com esta temos condição de determinar o volume total de água infiltrado no solo. A Ia com o tempo, também passará a assumir valores constantes, neste ponto encerra o processo de determinação tanto da Ia como da VI.

As equações gerais para determinação de VI e Ia, seguem o modelo empírico de Kostiakow como mostrado a seguir:

Onde:

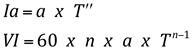
Ia – infiltração acumulada (cm);

a, n – coeficientes relativos às características do solo;

T – tempo acumulado (min);

Vi – velocidade de infiltração (cm/h)

60 – constante de transformação de unidade (minutos para horas).

Este modelo é limitado para situações em que há disponibilidade de dados de infiltração observados para a determinação dos parâmetros da equação.

Condições intrínsecas do solo:
– cobertura vegetal;

– estado de agregação das partículas do solo, seja por práticas culturais, efeito das irrigações ou precipitações;

– compactação;

– erodibilidade.
Condições extrínsecas do solo:
– textura;

– adensamento de perfis;

– flora e a fauna do solo;

– conteúdo de água (umidade do solo).
Condições de entrada de água
– duração da aplicação de água;

– carga hidráulica;

– qualidade e a temperatura da água.

Para determinação da infiltração da água no solo faz-se um teste de infiltração, onde existem diferentes métodos de determinação, como descrito a seguir.

Além da estrutura do solo, como já citado anteriormente, a infiltração de água pode ser afetada por outros fatores, como a umidade, posição do lençol freático, etc.

A infiltração é afetada pelo teor de umidade do solo, de modo que quanto mais seco o solo, maior o gradiente de potencial entre a frente de umedecimento e a camada de solo situada abaixo, e mais rápida a sua absorção.

O lençol freático próximo a superfície reduz a velocidade de infiltração em virtude de umedecer as camadas adjacentes.

A presença de uma camada endurecida ou impermeável afeta o avanço da frente de umedecimento, conseqüentemente a velocidade de infiltração, cuja redução dependerá da profundidade da camada endurecida e mais rápida será sua saturação.

A passagem da água através do solo pode arrastar partículas que irão bloquear os poros próximos a superfície. A compactação produzida pelas máquinas, veículos entre outros também tende a diminuir e bloquear os poros do solo causando essa diminuição na velocidade de infiltração.

O desenvolvimento radicular nas camadas superficiais beneficia o processo de infiltração, particularmente no caso de solos argilosos, cujas raízes abrem caminhos no interior do solo que facilitam a infiltração podendo provocar um aumento na velocidade de infiltração.

Uma observação importante na determinação de infiltração de água no solo, é que os testes têm sua melhor eficiência logo após uma chuva, pois o solo se encontrará um teor de umidade próximo a capacidade de campo, não ocorrendo variações acentuadas na determinação, e diminuindo o tempo de coleta dos dados no campo.

c) Teste de infiltração de água no solo

Antes de qualquer projeto que levem em consideração a infiltração de água no solo, é determinarmos o comportamento da água no solo através da velocidade de infiltração de água no solo através do teste de infiltração de água no solo.

A infiltração de água no solo pode ser tratada de duas maneiras:

quantidade de água que entra no solo → Ia
velocidade com que a água entra no solo → VI

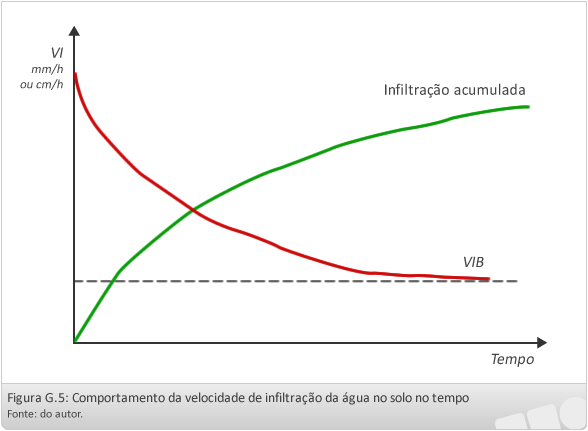
Observando a Figura 3, obtida após um teste de infiltração de água no solo, podemos observar o comportamento da infiltração. No início, à medida que a água é colocada no solo, a VI é alta (linha vermelha), ou seja, a água infiltra rapidamente, devido ao solo estar seco (poros vazios), com o decorrer do tempo essa infiltração vai diminuindo gradativamente, pois os poros já estão sendo preenchidos por água. A VI diminui até um ponto de estabilização, onde a velocidade de infiltração de água passa a ser constante, a este ponto é dado o nome de VIB (velocidade de infiltração básica), que é a infiltração na condição de saturação do solo.

Método dos cilindros concêntricos

Para este método de determinação da infiltração de água no solo são utilizados dois anéis de diâmetros diferentes. Estes anéis são inseridos no solo concentricamente, ou seja, o anel de menor diâmetro é fixado no solo primeiramente até uma profundidade de 15 cm, o anel de maior diâmetro também fixado a 15 cm de profundidade, envolvendo o anel de menor diâmetro.

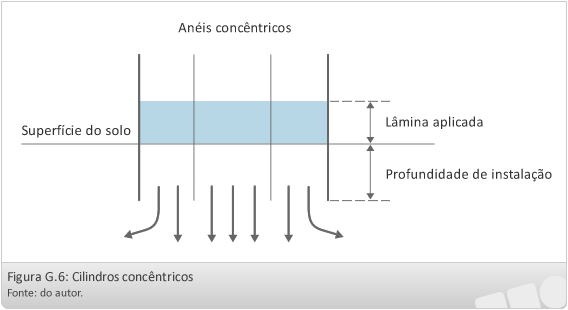
- Procedimentos

Instalar os dois cilindros no solo, com a ajuda de um batente, normalmente de chapa metálica circular pouco maior que os cilindros, até uma profundidade entre 10 e 15 cm;
Instalados os cilindros, realiza-se uma coleta com trado, em área próxima, amostras de solo, nas profundidades de 0-15 cm e 15-30 cm, para determinação da umidade gravimétrica, pois esta interfere na infiltração da água no solo;
Colocar uma lona de plástico no interior do cilindro interno, ajustando-a bem ao solo e à parede do cilindro;
Colocar água no cilindro interno, como ele esta recoberto com lona plástica, não há infiltração de água no solo. A água deve ser adicionada até que forme uma lâmina, no seu interior de aproximadamente 7,5 cm de espessura;
Instalar a régua graduada, com flutuador, no cilindro interno;
Ler o posicionamento do nível da água na régua graduada e registrar o valor na folha de dados (essa leitura corresponderá ao tempo zero, isto é, tempo inicial de contagem);
Introduzir água no espaço existente entre o cilindro interno e o externo, até que forme uma lâmina de aproximadamente 5 cm. Deve-se manter o cilindro infiltrômetro (cilindro interno) rodeado de água, para evitar que a água contida nele adquira, por ocasião da infiltração (depois de retirada a lona plástica) movimento horizontal de água no solo, isto é, fuga lateral por baixo do cilindro, acarretando erro na determinação da taxa de infiltração;
Retirar a lona plástica do cilindro interno e acionar o cronômetro imediatamente (início da marcação do tempo de infiltração, isto é, instante inicial to = 0 – coluna 1 da folha de dados);
As colunas 1, 2 e 3, são preenchidas em função do tempo de aquisição dos dados, ou seja, na coluna 1 o horário de cada leitura na régua graduada, na coluna 2 o tempo acumulado em cada medição e na coluna 3 o tempo transcorrido em cada medição;
Com o auxílio da régua graduada provida de flutuador, ler o posicionamento do nível da água (h) aos 1, 2, 3, 4, 5, 10, 20, 30, 45, 60, 90, e 120 minutos a contar do instante zero, e após se for preciso, continuar as leituras com intervalos de uma hora, até que a velocidade de entrada de água no solo seja quase constante. Registrar os valores na coluna 4 da folha de dados;
Quando na seqüência de leituras (nos tempos indicados), se constatar que o nível da água no interior do cilindro interno baixou mais ou menos 5 cm, adicionar, imediata e cuidadosamente, água naquele cilindro, até repor o nível inicial. Completada a adição de água, medir, em seguida, com o auxílio da régua graduada, o novo posicionamento do nível água (h’) no cilindro interno e registrar na folha de dados (coluna 5), na linha correspondente ao instante em que a água foi acrescentada (mesmo instante da leitura anterior – última leitura da coluna 3, antes do acréscimo de água);
Com os dados obtidos a campo (colunas 1, 2, 3, 4 e 5 da folha de dados) calcular e registrar os demais valores da folha de dados, como descrito a seguir;
Preencher a coluna 6, determinando a lâmina de água infiltrada (Dh), em centímetros, dentro de cada intervalo de tempo, pela diferença entre os valores seqüenciais de h (coluna 4), isto é, 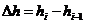Obs.: quando houver reposição de nível de água no cilindro interno, substituir, no subseqüente cálculo de Dh , o valor de hi-1 da expressão anterior pelo correspondente valor de h’i-1, onde este é a leitura do nível de água recomposto (coluna 5);
Completar o preenchimento, se for o caso, da coluna 6, determinando o intervalo de tempo (Dt), em minutos, entre as leituras consecutivas, pela diferença entre valores seqüenciais de t (coluna 1), isto é, ;
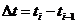Determinar a equação da lâmina de água infiltrada (lâmina acumulada)
Determinar a equação da taxa de infiltração média;
Determinar a equação da taxa de infiltração.

- EXEMPLO

1	2	3	4	5	6	7	8	9
Hora	T (min)	DT (min)	Leitura (cm)	Recarga (cm)	DiferenÇa (cm)	Ia (cm)	Vim (cm/h)	VI (cm/h)
14:10	0	-	7,0		-	0
14:11	1	1	6,7		0,3	0,3	18,0	18,0
14:12	2	1	6,5		0,2	0,5	15,0	12,0
14:13	3	1	6,4		0,1	0,6	12,0	6,0
14:14	4	1	6,3		0,1	0,7	10,5	6,0
14:15	5	1	6,2		0,1	0,8	9,6	6,0
14:20	10	5	5,8		0,4	1,2	7,2	4,8
14:25	15	5	5,5		0,3	1,5	6,0	3,6
14:30	20	5	5,2		0,3	1,8	5,4	3,6
14:40	30	10	4,7		0,5	2,3	4,6	3,0
14:55	45	15	4,1	7,2	0,6	2,9	3,9	2,4
15:10	60	15	6,7		0,5	3,4	3,4	2,0
15:40	90	30	5,8		0,9	4,3	2,9	1,8
16:10	120	30	5,0		0,8	5,1	2,6	1,6
16:40	150	30	4,3	7,3	0,7	5,8	2,3	1,4
17:10	180	30	6,7		0,6	6,4	2,1	1,2
17:40	210	30	6,1		0,6	7,0	2,0	1,2

Horário em que foram feitas as leituras na régua;
Tempo acumulado de cada medição;
Tempo transcorrido desde a medição anterior;
Altura de água medida no anel interno;
Altura de água medida no anel interno, após recarga;
Redução da lâmina de água em cada período de tempo;
Infiltração acumulada;
Taxa de infiltração média (infiltração acumulada / tempo acumulado);
Taxa de infiltração (redução da lâmina / ΔT)

- CÁLCULOS

- Equação da Lâmina de água infiltrada (lâmina acumulada):

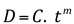
Onde:

D = lâmina de água infiltrada, acumulada (cm), no tempo;

C = lâmina de água infiltrada (cm), no primeiro minuto;

t = tempo, em minutos;

m -= expoente da equação (0<m<1).

Trata-se de obter a função D = f(t); devemos determinar, pois, os valores dos parâmetros C e m da equação dada. Para tanto proceder como segue.

Faremos o ajuste de curvas e linearização de Equações Matemáticas.

Em papel log-log, assinalar no eixo das abscissas, os valores de tempo, em minutos constantes da coluna 1da folha de dados, e no eixo das ordenadas à esquerda do gráfico, os correspondentes valores da lâmina acumulada, em centímetros, constantes da coluna 8 na folha de dados.

Plotar, no gráfico, os pontos resultantes dos lançamentos feitos (coordenadas anteriores).

Traçar, graficamente, a reta de melhor ajuste, (reta com coeficiente angular positivo).

Obter graficamente, os valores de A (log A = a = coeficiente linear da reta) e de b (coeficiente angular da reta). Para obter A, ler, no eixo das ordenadas, o valor da intersecção da reta com o mencionado eixo (ordenada na origem). Para obter b, tomar o valor das abscissas de dois pontos da reta, suficientemente afastados, e os correspondentes valores das ordenadas, formando um triângulo retângulo com a reta e através da relação de triângulos se obtém o valor de b, como mostra a figura a seguir.

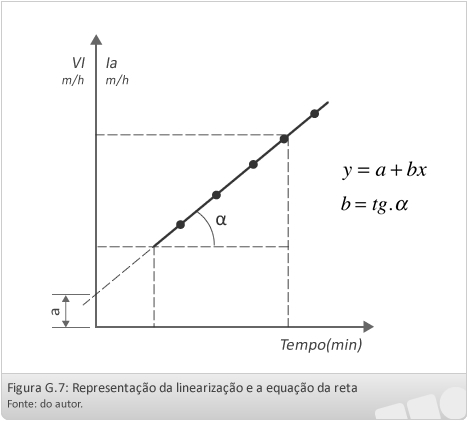
Uma maneira simples de determinarmos o valor de b é traçarmos uma reta na horizontal em qualquer ponto da reta VI ou Ia, com um comprimento conhecido em cm, como por exemplo 10 cm, depois medimos sua reta na vertical até encontrar a reta VI ou Ia com auxílio de uma régua, de posse destes dois valores teremos o valor de b pela tangente de a, como mostra a figura 6.

- Equação da taxa de infiltração instantânea:

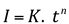
onde:

I = taxa de infiltração instantânea (cm/h), num instante qualquer de t;

K = taxa de infiltração instantânea (cm/h), ao final do primeiro minuto;

t = tempo em minutos;

n = expoente da equação (-1<n<0).

Trata-se de obter a função I = f(t), devem-se determinar, os valores dos parâmetros K e n da equação dada,da seguinte maneira:

Calcular K pela expressão: K=60.C.m , onde C e m são os parâmetros da equação anterior.

Calcular n pela expressão: n=m-1.

Introduzir os valores numéricos de K e n na equação.

Plotar, por pontos, a equação descrita no mesmo papel log-log utilizado para a obtenção da primeira equação (deverá resultar outra reta, porém com coeficiente angular negativo).

- Equação da taxa de infiltração acumulada:

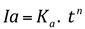
onde:

Ia = taxa de infiltração acumulada (cm/h), num intervalo de tempo qualquer t;

K_a = taxa de infiltração acumulada (cm/h), no primeiro minuto;

t = tempo em minutos;

n = expoente da equação (-1<n<0).

Trata-se de obter a função Ia = f(t); devem-se determinar os valores dos parâmetros Ka e n da equação dada.

Calcular Ka pela expressão: K_a=60.C , sendo C já conhecido da primeira equação;

Fazer n igual ao expoente da equação anterior.

Introduzir os valores numéricos de Ka e n na equação.

Plotar, por pontos, esta equação, no mesmo papel log-log utilizado para as equações anteriores (deverá resultar em uma reta com coeficiente angular negativo).

Unidade G - Infiltração