Modelos de escoamento superficial
Hidrogramas unitários sintéticos
O hidrograma é uma constante da bacia hidrográfica, refletindo as suas propriedades com relação ao escoamento superficial.
As diversas características físicas da área drenada devem, em maior ou menor grau, influenciar as condições de escoamento e contribuir para a forma final do hidrograma unitário. Esse fato, aliado à frequente necessidade de estabelecer relações hidrológicas em rios desprovidos de estações hidrométricas, sugeriu o estudo da síntese de hidrogramas, independentemente da existência de dados hidrológicos, e desenvolvimento de métodos para a obtenção do chamado hidrograma unitário sintético.
Características físicas da bacia hidrográfica que tem influência sobre o fluviograma resultante de uma precipitação:
- Área: o volume escoado é diretamente proporcional à superfície drenada pela própria definição do hidrograma unitário.
- Declividade: de maneira geral, quanto maior a declividade, maior a velocidade de escoamento e relativamente mais altos os picos do hidrograma.
- Dimensões e rugosidade do canal: quanto mais largos os rios, maior o volume acumulado e, consequentemente, mais o efeito moderador sobre a onda de cheia. Canais de menor resistência devem conduzir a cheias mais rápidas e altas.
- Densidade da rede de drenagem: maior densidade tende a sugerir um escoamento mais rápido, entretanto, este efeito pode ser contrabalançado pelo aumento do volume represado temporariamente nos canais.
- Forma:uma bacia sensivelmente alongada condicionaria a um hidrograma menos pronunciado do que outra em forma de leque, em que a drenagem poderia se dar mais rapidamente.
O recobrimento vegetal, o tipo de solo, a capacidade de acumulação temporária do volume escoado são outros tantos fatores que podem influenciar as características do escoamento superficial, condicionando a forma do hidrograma resultante.
De maneira geral, os modelos sintéticos obedecem a uma sistemática mais ou menos análoga, como segue:
- Seleção das características básicas da bacia hidrográfica a serem consideradas e definição quantitativa das mesmas.
- Seleção de diversas bacias em que se podem definir aquelas características, abrangendo uma certa gama de variação.
- Pesquisa de correlações entre as características físicas e a configuração das ondas de cheia observadas nas diversas bacias.
- Seleção e representação gráfica ou matemática das correlações mais significativas, permitindo sua utilização para a predição do hidrograma unitário em bacias que não dispõem de medidas de vazão.
Estudaremos o método de Snyder, um dos mais conhecidos, que ilustra a natureza e a característica desse tipo de estudo; o método de Commons, cuja simplicidade o torna bastante útil, mesmo considerando-se que depende do conhecimento prévio da vazão de ponta; e finalmente o método de Getty e McHughs, dos mais recentes, o qual pode se constituir em uma complementação conveniente ao método de Commons.
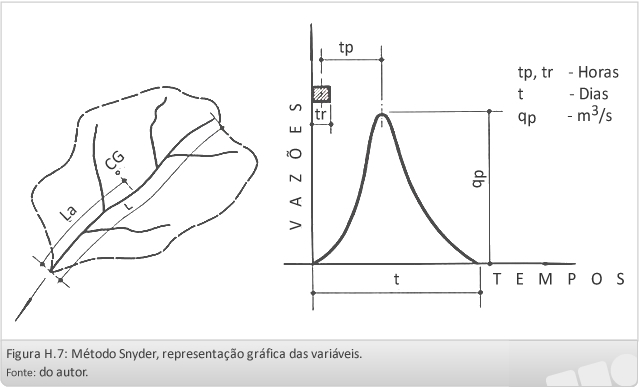
Método de Snyder
Para definir o hidrograma unitário, estabeleceu-se equações que fornecem o tempo de retardamento, a vazão de pico e a duração total do escoamento, ou seja, a base do hidrograma.
O tempo de retardamento (tp), é definido como o tempo entre o centro de massa da precipitação efetiva e o pico do hidrograma. É distinto, portanto, da noção apresentada no estudo do hidrograma unitário, em que considerava o centro de massa do hidrograma em vez do ponto de máxima vazão.
Snyder obteve a seguinte expressão:
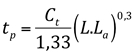
Onde:
L = Comprimento da bacia em km, medido ao longo do curso principal do rio, desde o ponto considerado até o divisor.
La = Distância do centro de gravidade da bacia em km, medido ao longo do curso principal, desde a seção considerada até a projeção do centro de gravidade sobre o rio.
Ct = Coeficiente numérico variável entre 1,8 e 2,2. É interessante notar que Linsley, em estudo análogo para bacias da vertente oeste da Serra Nevada, na Califórnia, obteve valores entre 0,7 e 1,0;
tp = Tempo de retardamento da bacia em horas.
O hidrograma sintético de Snyder considera que o tempo de duração da precipitação que provoca (tr) é igual a:

A vazão máxima (Qp) é dada pela expressão:
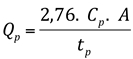
Sendo A a área da bacia em km2 e Cp um coeficiente numérico variável entre o,56 e 0,69. Para a Califórnia, Linsley constatou valores entre 0,35 e 0,50.
Quando se consideram precipitações de duração (tR) superior ao tempo (tr) dado na equação anterior, o valor de tp também da equação anterior deve ser substituído por t’p:
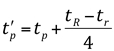
A expressão de t’p é empírica e não foi completamente justificada pelo autor. A base do hidrograma (t) é dada pela expressão:
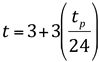
Em que t é expresso em dias e tp em horas. Esta equação cresce, igualmente, de maiores justificativas e deve ser encarada com reservas.
Pela combinação das equações de tr e t’p e levando-se em conta a definição de tr, pode-se obter o tempo desde o início da precipitação até o momento da máxima vazão (tp).
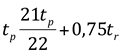
Obtidos os valores de tp, Qp e t, o hidrograma unitário pode ser desenhado a sentimento, com cuidado de se manter igual à unidade (1 cm) o volume sob a curva.
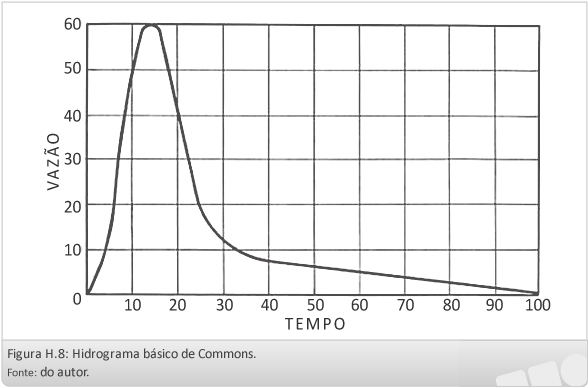
Método de Commons
O método de Commons, ou do hidrograma básico, consiste simplesmente em um hidrograma adimensional, com base em observações de inúmeras cheias no Texas, que pretende dar uma aproximação satisfatória para hidrogramas de cheias em bacias de qualquer superfície.
A base do hidrograma é dividida em 100 unidades e sua maior altura em 60 unidades. A área sob a chuva é de 1196,5 unidades ao quadrado.
O hidrograma básico exige o conhecimento da vazão de ponta ou da escala dos tempos, fornecendo essencialmente a distribuição do volume do escoamento superficial ao longo do tempo.
Se a máxima vazão for conhecida, a unidade da vazão será dada por:
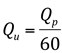
Dividindo-se o volume total escoado (no caso, 1 cm sobre a área da bacia, 0,01xA, expresso em m3) por 1196,5, obtém-se a unidade ao quadrado, que, dividida por Qu, fornece o valor da unidade de tempo tu.
De forma análoga, conhecendo-se tp ou t e o volume total, pode-se obter Qu e, portanto:
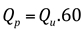
Observa-se que não existe nenhuma referência à precipitação que dá origem ao hidrograma. Pressupõem-se, com base nos conhecimentos advindos do estudo do hidrograma unitário, que a duração da precipitação a ser considerada não deve ultrapassar tp/4; de maneira geral, pode ser admitida como entre 1/6 e 1/3 de tp.
Método de Getty e McHughs
Baseado em observações de 42 estações hidrométricas em terrenos ondulados do Arkansas e Missouri, E.U.A., em bacias hidrográficas de 1,6 a 5260 km2, esse método relaciona a máxima vazão, expressa em termos de descarga específica (m3/s.km2), aos comprimentos L e La , já definidos para o método de Snyder, à área da bacia e, ainda, à declividade do rio principal (S). Para cada área, a vazão é expressa em função:
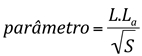
Os resultados são apresentados de forma gráfica, onde:
qp – vazão de ponta em m3/s.km2;
L, La – em km;
S – declividade efetiva da bacia em m/km;
A – área da bacia em km2.

A declividade efetiva é definida com base no trabalho de Taylor e Schwartz, sendo calculada a partir da expressão:
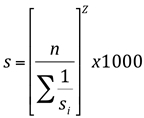
Onde S é a declividade efetiva em m/km; n, o número de incrementos iguais do curso de água mais longo; e Si, a declividade de cada incremento de canal em m/m.