Vazões máximas com base em precipitações
A ausência de dados de vazão é o caso mais comum que os engenheiros hidráulicos/ hidrólogos, envolvidos no dimensionamento de obras hidráulicas, enfrentam nas atividades do dia a dia.
Métodos indiretos mais utilizados:
- Método racional;
- Método do hidrograma unitário;
- Método de SoilConservation Service (SCS).
Todos os métodos indiretos estimam as vazões a partir dos dados de chuva que são menos escassos do que os dados de vazão; desta forma, cabe rever, inicialmente, alguns conceitos de chuvas intensas.
Método racional
Serve para a estimativa da vazão máxima de cheia (pico) a partir de dados de precipitação. Utilizado apenas para pequenas bacias, é o método mais utilizado em drenagem urbana (dimensionamento de bueiros, galerias, etc.), drenagem de rodovias, ferrovias, entre outros.
O método racional é largamente utilizado na determinação da vazão máxima de projeto para bacias hidrográficas pequenas de até 500 ha.
Os princípios básicos do método racional são:
- Considerar a duração da precipitação intensa de projeto igual ao tempo de concentração da bacia;
- Adotar um único coeficiente de escorrimento superficial (C), estimado com base nas características da bacia hidrográfica;
- Não avalia o volume da cheia e a distribuição temporal das vazões.
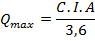
Q = pico de vazão, m3/s.
I= intensidade média de precipitação sobre a bacia, com duração igual ao tempo de concentração da bacia, mm/h.
A = área de drenagem da bacia, km2.
C= coeficiente de "runoff".
- Intensidade: O tempo de concentração pode ser estimado por uma equação derivada com base na onda cinemática para precipitação constante.
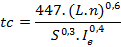
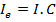
Onde:
tc: tempo de concentração em minutos;
L: comprimento do rio em km;
n: rugosidade de Manning;
S: declividade (m/m);
Ie: precipitação efetiva em mm/h;
Cobertura da bacia |
n |
Asfalto suave |
0,012 |
Asfalto ou concreto |
0,014 |
Argila compactada |
0,030 |
Pouca vegetação |
0,020 |
Vegetação densa |
0,35 |
Vegetação densa e floresta |
0,40 |
Tabela J.2 - Coeficiente de Manning Fonte: Tucci (2004).
A precipitação é obtida das curvas de intensidade, duração e frequência do local em estudo. Quando a equação anterior de cálculo do tempo de concentração (tc) o processo de cálculo torna-se interativo, pois para determinar a intensidade I é necessário conhecer a sua duração, que é igual ao tempo de concentração. Quando a intensidade é expressa na forma da equação do tipo
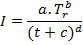
Onde:
Tr: tempo de retorno;
a, b, c, d: coeficientes que dependem do local;
t: duração.
Como no método Racional a duração da precipitação é considerada igual ao tempo de concentração, pode-se substituir a equação do tempo de concentração(tc) vista anteriormente na equação de Intensidade (I).
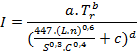
A estimativa do coeficiente C é baseada em tabelas e tem alguns aspectos subjetivos .
O tempo de concentração e o tempo de pico também podem ser estimados por equações empíricas estabelecidas em diferentes regiões. Existem expressões para cada uma destas variáveis além de relações entre si. A seguir veremos algumas equações.
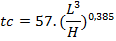
Onde:
tc: tempo de concentração em minutos;L: comprimento do rio em km;
H: diferença de nível entre o ponto mais alto da bacia e a seção principal (exutório).
O tempo de pico, tempo de retardo e tempo de concentração segundo Mockus citado por Tucci (2004), se relacionam segundo as seguintes equações:
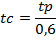
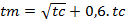
O tempo de pico tem sido expresso por uma função do tipo:
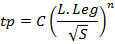
Onde:
Leg – comprimento do rio principal da foz até o ponto mais próximo ao centro de gravidade da bacia;
L – comprimento do rio;
S – declividade;
C, n – são parâmetros estimados para cada local de interesse.
O coeficiente C pode ser obtido pela tabela 1, em função do tipo de cobertura existente na bacia hidrográfica, tipo de solo, da declividade do talvegue e do tamanho da bacia hidrográfica.

Tabela J.3 - Coeficiente de escoamento (c), para áreas agrícolas inferiores a 500 ha, em função da topografia, da cobertura e do tipo de solo.
Fonte: Daker (1983)
Normalmente as bacias hidrográfica apresentam mais de um tipo de cobertura vegetal, tipo de solo e mais de uma declividade, neste caso são feitos cálculos levando-se em consideração estes aspectos da seguinte maneira: por exemplo se estivermos calculando a vazão máxima de uma bacia hidrográfica com três tipos de coberturas vegetais, dois tipos de solo e cada área com uma declividade, calculamos um coeficiente de escorrimento superficial médio, ou seja, em função do tipo de cobertura que se tem, da declividade e do tipo de solo, procura-se na tabela o coeficiente C correspondente, após multiplica-se cada um dos coeficientes pela sua respectiva área, obtém-se três valores, em seguida somam-se estes três valores e divide-se pela área total e se obterá um novo coeficiente de escorrimento levando em consideração as diferentes características da bacia hidrográfica. Equacionando este sistema teríamos:
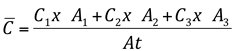
Onde:
C1 = coeficiente de escorrimento da Área 1 em função da declividade, tipo de solo e cobertura vegetal;
C2 = coeficiente de escorrimento da Área 2 em função da declividade, tipo de solo e cobertura vegetal;
C3 = coeficiente de escorrimento da Área 3 em função da declividade, tipo de solo e cobertura vegetal;
A1 = Área 1 da bacia hidrográfica em hectare;
A2 = Área 2 da bacia hidrográfica em hectare;
A3 = Área 3 da bacia hidrográfica em hectare;
At = Área total da bacia hidrográfica em hectare.
Tipo de Área |
C |
1 Topografia: |
0,30 |
2 Solo |
0,10 |
3 Cobertura |
0,10 |
Tabela 2 : Valor de C para áreas rurais (Tucci, 2004).
Zonas |
C |
Edificação muito densa: |
0,70 – 0,95 |
Edificação não muito densa: |
0,60 – 0,70 |
Edificações com poucas superfícies livres: |
0,50 – 0,60 |
Edificações com muitas superfícies livres |
0,25 – 0,50 |
Subúrbios com alguma edificação |
0,10 – 0,25 |
Matas, parques e campos de esportes |
0,05 – 0,10 |
Tabela 3 : Valor de C adotado pela prefeitura de São Paulo (Tucci, 2004).
Tempo de retorno (anos) |
Cf |
2 a 10 |
1,00 |
Tabela 4 : Fator de correção de C (Tucci, 2004).
Superfície |
C |
|
Intervalo |
Valor esperado |
|
Pavimento: |
0,70 – 0,95 |
0,83 |
Cobertura – grama solo arenoso: |
0,05 – 0,10 |
0,08 |
Grama – solo pesado: |
0,13 – 0,17 |
0,15 |
Tabela 5 : Valor de C (Tucci, 2004).
Método da hidrógrafa unitária
Princípio básico
"Se duas chuvas idênticas ocorrerem em uma bacia hidrográfica, as hidrógrafas de escoamento superficial serão idênticas."
Definição
É a hidrógrafa resultante de uma precipitação efetiva com altura unitária (1 cm, 1 mm, 1 inch, etc.).
Princípio da linearidade e superposição:
Cálculo da hidrógrafa unitária para chuva com duração T horas (hidrógrafas unitárias para durações diferentes também são diferentes):
A partir de dados de uma cheia com duração de chuva T horas:
a) Separa-se o escoamento superficial.
b) Determina-se o volume de escoamento superficial, que é igual ao volume de chuva efetiva.
c) Calcula-se a altura de chuva efetiva, dividindo o volume pela área da bacia.
d) Obtêm-se a hidrógrafa unitária de duração T horas, pela divisão das ordenadas da hidrógrafa de escoamento superficial pela altura efetiva.
O método da hidrógrafa unitária é recomendado para bacias de pequeno e médio porte que possuem extenso período de registro de precipitações e curto período de dados de vazões. Faz-se estudo probabilístico dos dados de chuva, e as chuvas de projeto são aplicadas à hidrógrafa unitária, possibilitando a previsão de vazões.
Previsão de vazões a partir de hidrógrafa unitária:
a) Cálculo da chuva efetiva.
b) Multiplicação da altura pelas ordenadas da hidrógrafa unitária, obtendo-se as ordenadas de escoamento superficial.
c) Soma das ordenadas de escoamento superficial com ordenadas de escoamento subterrâneo, obtendo-se as ordenadas de escoamento total.
Em caso de chuvas seguidas, com duração T horas cada, aplica-se separadamente a hidrógrafa unitária de duração T horas e superpõem-se as hidrógrafas de escoamento superficial resultantes.
Os métodos da Curva-S (hidrógrafa unitária para chuva com duração infinita) e da hidrógrafa unitária instantânea (hidrógrafa unitária para chuva com duração tendendo a zero), servem para transformar hidrógrafas unitárias de uma duração de chuva para outras durações. Mendonça (1977) analisou e programou dez métodos de cálculo de hidrógrafa unitária, Mendonça e Campos (1989) adaptaram estes métodos em "software" em linguagem BASIC.
Hidrógrafas unitárias sintéticas
São aquelas cujas ordenadas são obtidas a partir de características físicas da bacia, com finalidade de utilização em bacias onde não existam registros de vazões. Vários métodos foram propostos por hidrólogos para este fim. Entre eles, os mais utilizados são os de Snyder e o do U.S. SoilConservation Service. Snyder estabeleceu as seguintes expressões para a hidrógrafa unitária com altura de chuva unitária 1 inch (2,54 cm).
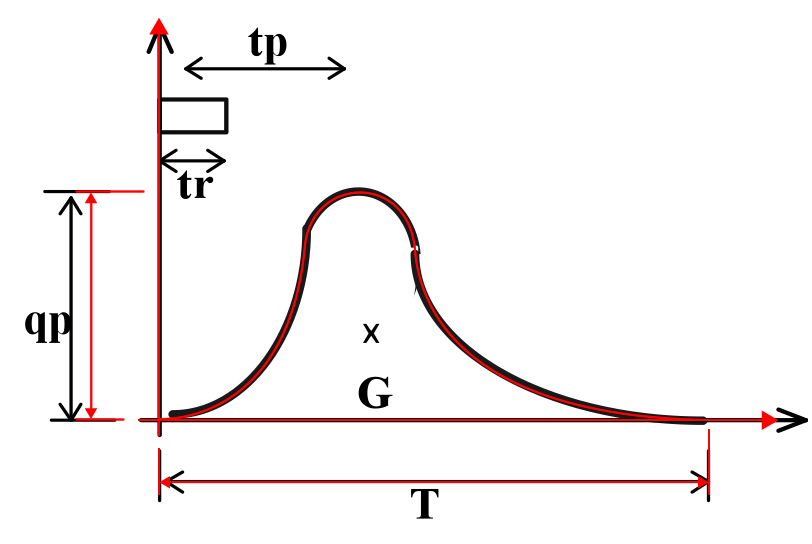
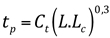
tp= tempo de retardamento da bacia (horas) = tempo entre o centróide da chuva e o centróide do escoamento superficial.
Ct= coeficiente que varia entre 1,8 e 2,2 (para as bacias dos montes Apalaches).
L = comprimento do rio principal.
Lc = distância do ponto do rio principal mais próximo do centróide da bacia até a saída da mesma.
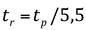
tr= duração da chuva, em horas
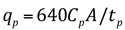
qp= vazão máxima da hidrógrafa unitária (ft3/s).
A = área da bacia em milhas quadradas.
Cp = varia entre 0,56 e 0,69.
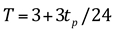
T = tempo base do escoamento superficial (dias).