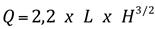Definição
Chama-se vazão ou descarga, numa determinada seção, ao volume de líquido que atravessa a seção na unidade de tempo. O fluído pode ser líquido gás ou vapor.
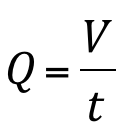
Onde:
Q = vazão (m3/s)
V = volume (m3)
t = tempo (s)
A medida e controle de vazão tem suas mais diversas utilidades tais como, em sistemas de abastecimento de água, estudo de lançamento de esgotos, instalações hidroelétricas, obras de irrigação, etc. A medição de vazão encontra importantes aplicações do transporte de fluídos, nos serviços públicos e na indústria em geral, para controle de relação, bateladas, balanços de massa, contribuindo para a qualidade e otimização de controle de processos. Outras aplicações estão os medidores domésticos (hidrômetro, medidor de gás) e os medidores de combustíveis (bombas de postos de abastecimento).
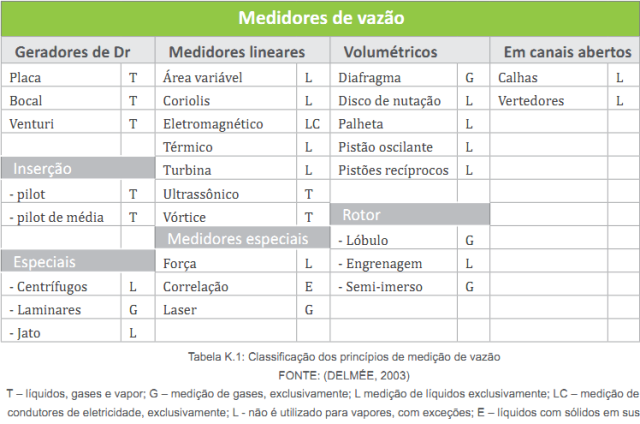
Tabela 1: Classificação dos princípios de medição de vazão (DELMÉE, 2003).
T – líquidos, gases e vapor;
G – medição de gases, exclusivamente;
L medição de líquidos exclusivamente;
LC – medição de líquidos condutores de eletricidade, exclusivamente; - não é utilizado para vapores, com exceções;
E – líquidos com sólidos em suspensão.Neste capítulo veremos alguns os métodos mais utilizados e tradicionais na medição de vazão, embora existam muitos outros. Os métodos mais utilizados são os seguintes:
Processos de medidas em condutos forçados:
- Hidrômetro;
- Medidores diferenciais:
- Diafragma;
- Medidor Venturi;
- Tubo de Pitot;
- Orifícios;
- Bocais;
- Vertedores;
- Medidores de regime crítico (medidor Parshall).
Processos de medição direta (condutos livres):
Medidas em condutos forçados
- Hidrômetro
Aparelho destinado à medida da quantidade de água que escoa em intervalos de tempo – intervalos relativamente longos.
Este tipo de medidor é empregado geralmente em instalações prediais e industriais. Os hidrômetros nos fornecem a leitura direta do volume de fluído que está escoando.
Existem dois tipos de hidrômetros:
- Hidrômetro de velocidade – tipo turbina
- Vantagens:
- Mais baratos;
- Mais simples;
- Fácil manutenção;
- Insensíveis às impurezas da água.
- Desvantagens:
- Limite de sensibilidade e exatidão menores.
- Hidrômetro de volume – compartimento que enche e esvazia continuamente.
- Vantagens:
- Maior precisão;
- Maior sensibilidade;
- Indicado para pequenos consumos.
- Desvantagens:
- Mais caros;
- Sensíveis às impurezas da água;
- Difícil manutenção.
- Medidores diferenciais para condutos forçados:
Consistem numa redução na seção de escoamento de uma tubulação, de modo a produzir uma diferença de pressão, em consequência do aumento de velocidade.
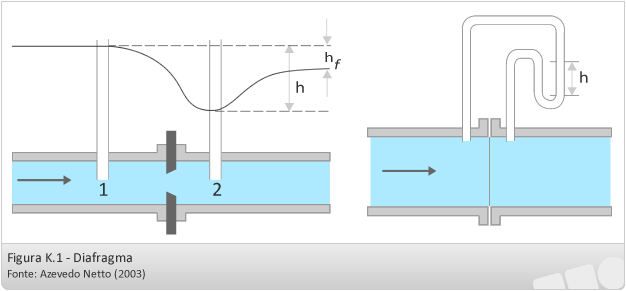
Diafragma
O tamanho do orifício do diafragma deve estar entre 30% e 80% do diâmetro da tubulação.
- Abaixo de 30% ocorre muita perda;
- Acima de 80% tem-se pouca precisão.
Deve ser instalado em trecho retilíneo horizontal ou vertical, sem perturbações, ou seja, derivações, curvas, registros, etc.
Equação para Diafragma:
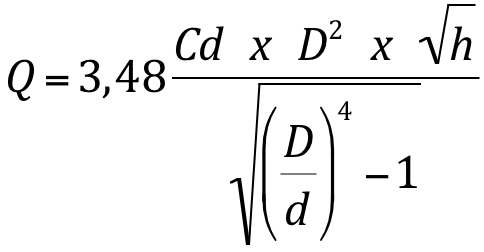
onde:
Q = vazão (m3/s)
Cd = coeficiente de descarga (Cd = 0,61)
D = diâmetro da canalização (m)
d = diâmetro da seção reduzida (m)
h = diferença de pressão entre os dois pontos de medida (mca)
Medidor Venturi:
Compreende três seções principais, uma peça com uma seção convergente, uma peça com uma seção divergente e uma seção intermediária que constitui a garganta ou seção estrangulada.
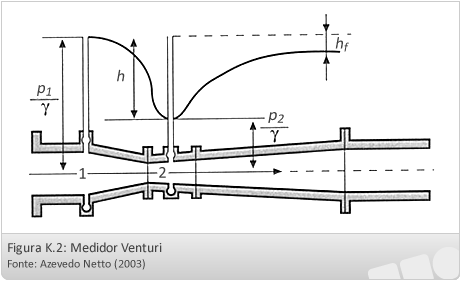
Características do medidor Venturi:
O diâmetro da garganta esta compreendido entre 1/4 e 1/3 do diâmetro da tubulação.
Classificação:
- Venturi longo – compreendido entre 5 e 12 vezes o diâmetro da tubulação;
- Venturi curto – compreendido entre 3,5 e 7 vezes o diâmetro da tubulação.
O medidor Venturi deve ser precedido de um trecho de canalização retilínea, pelo menos 6 vezes o diâmetro da canalização.
Equação para venturi:
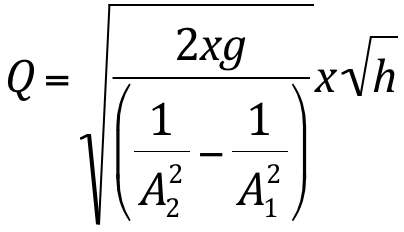
Onde:
Q = vazão (m3/s);
A2 = área da seção estrangulada (m2);
A1 = área da seção do conduto (m2);
h = diferença de pressão entre os dois pontos (mca).
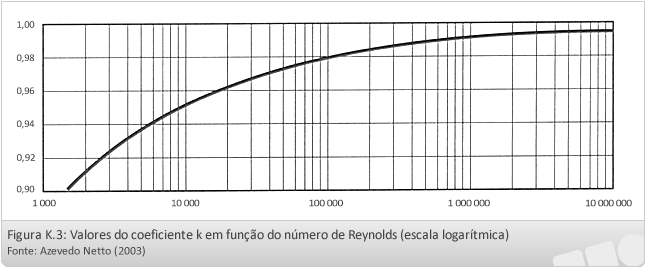
Deve-se ainda introduzir um coeficiente corretivo “k” de modo que:
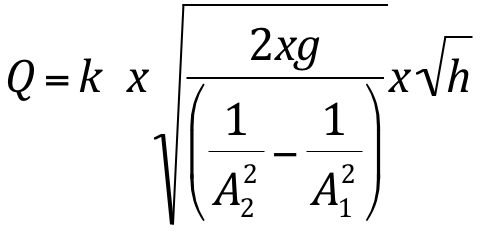
O coeficiente “k” depende do número de Reynolds, obtido em um gráfico de escala logarítmica.
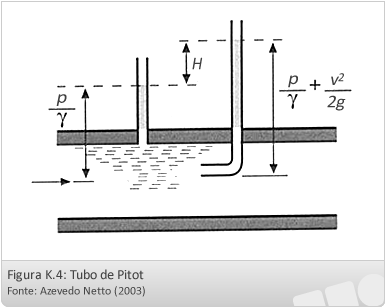
Tubo de Pitot:
O tubo de Pitot consiste na instalação de dois tubos piezométricos ao longo de uma canalização, sem que ocorra a diminuição da seção da tubulação. Um dos tubos é curvado em direção contrária ao escoamento do fluído.
A diferença é que o tubo de Pitot fornece a velocidade de escoamento do fluído dentro da canalização, sabendo-se o diâmetro da tubulação tem-se condição de se calcular a vazão de escoamento no conduto.
Equação para tubos de Pitot:
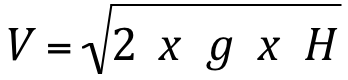
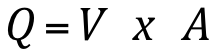 e
e 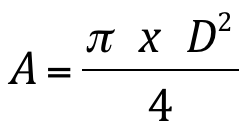
Onde:
V = velocidade de escoamento (m/s);
H = diferença de pressão entre os dois pontos (mca);
g = aceleração da gravidade (m/s2);
A = área da seção do conduto (m2).
Medidas de vazão direta:
Orifícios:
- Classificação dos orifícios:
Os orifícios são perfurações, geralmente de forma geométrica definida, feitas abaixo da superfície livre do líquido em paredes de reservatórios, tanques, canais ou canalizações.
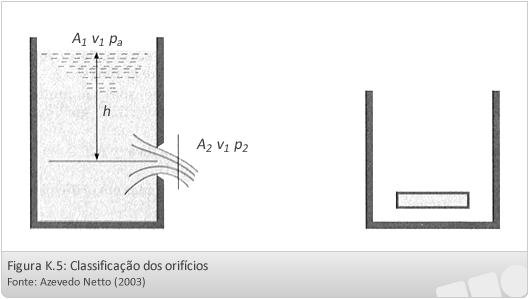
Os orifícios podem ser classificados quanto à forma e quanto ao tamanho:
- quanto à forma – circulares, retangulares, etc.
- quanto ao tamanho – pequenos ou grandes.
São considerados pequenos orifícios aqueles cujas dimensões são muito menores que a profundidade em que se encontram:
Dimensão vertical ≤ 1/3 da profundidade
Os orifícios ainda podem ser classificados quanto à natureza das paredes:
- Orifícios em parede delgada;
- Orifícios em parede espessa.
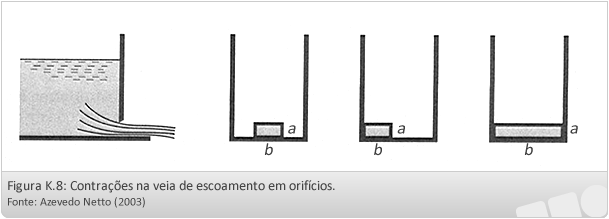
A parede é considerada delgada quando o jato líquido apenas toca a perfuração em uma linha que constitui o perímetro do orifício (Figuras a e b). Numa parede espessa, verifica-se a aderência do jato (Figura c).
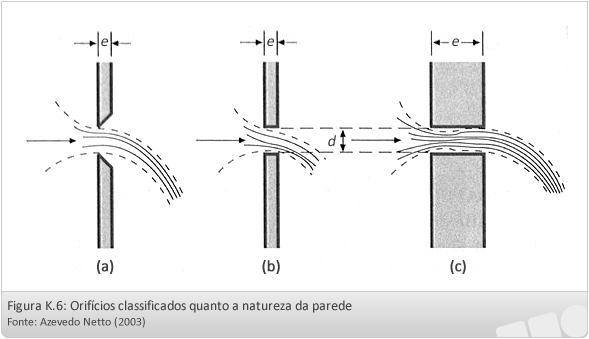
Os orifícios delgados são obtidos em chapas finas ou pelo corte em bisel. O acabamento em bisel não é necessário se a espessura e da chapa é inferior a 1,5 vezes o diâmetro d do orifício suposto circular ou a menor dimensão, se o orifício tiver outra forma:
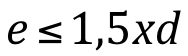
Onde:
e – espessura da chapa;
d – diâmetro ou menor dimensão do orifício.
Se e for maior que 1,5 vezes o diâmetro, o jato poderá se colar ao interior da parede, classificando-se o orifício como em parede delgada.
Se o valor de e estiver compreendido entre 2 e 3 vezes o diâmetro d teremos o caso de um Bocal.
Cálculo da vazão em orifícios:
- Orifícios de pequenas dimensões:
No caso de orifícios pequenos, pode-se admitir, sem erro apreciável, que todas as partículas atravessam o orifício animadas da mesma velocidade, sob a mesma carga h.
A equação utilizada para o cálculo da vazão em pequenos orifícios é a seguinte:
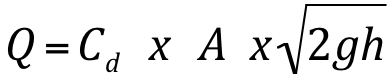
Onde:
Cd – coeficiente de descarga do orifício (tabelado);
A – área do orifício (m2);
h – carga sobre o centro do orifício (m).
Na prática é adotado um valor médio do Cd para orifícios em geral de 0,61.
- Orifícios de grandes dimensões:
Tratando-se de orifícios grandes, já não se pode admitir que todas as partículas que os atravessam estejam animadas da mesma velocidade, porquanto não se pode considerar uma carga única (h).
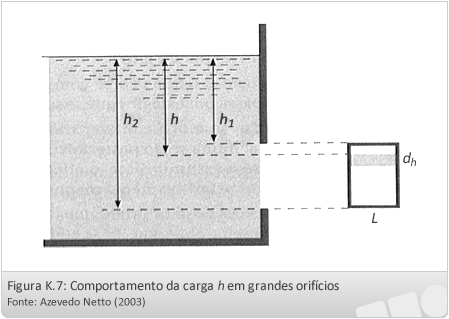
A equação que trata do cálculo de vazão para grandes orifícios é a seguinte:
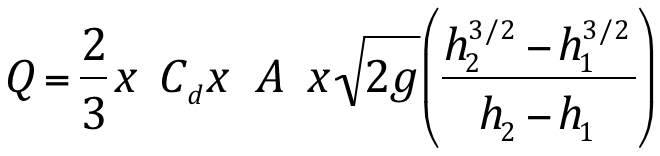
- Contração incompleta da veia
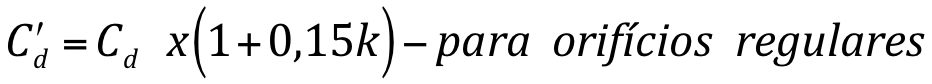

Ou pode ser obtido da seguinte forma, para orifícios retangulares:
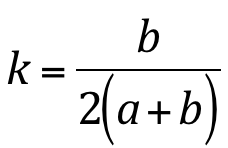 ;
;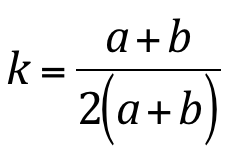 ;
;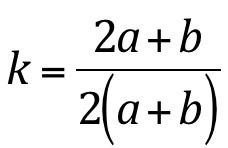
Onde a e b são as dimensões do orifício ilustrados na figura K.8.
Para orifícios circulares a equação é semelhante a de orifícios retangulares:
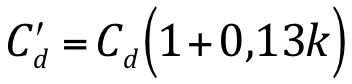
O coeficiente k para orifícios circulares junto a uma parede lateral é k = 0,25, para orifícios junto ao fundo k = 0,25, para orifícios junto ao fundo e uma parede lateral k = 0,50, para orifícios junto ao fundo e duas paredes laterais k = 0,75.
- Orifícios afogados em paredes delgadas:
Diz-se que um orifício está afogado quando a veia escoa em massa líquida abaixo do nível do fluído, ou seja, o orifício está submerso, como mostra a figura:
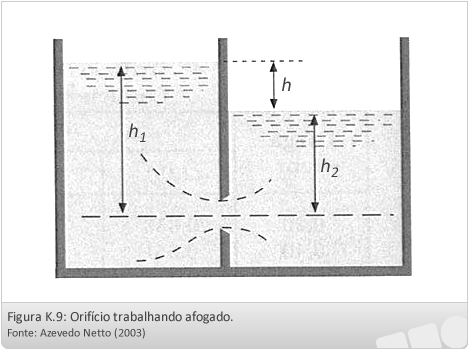
A expressão de Torricelli pode ser mantida, porém, a carga h deve ser considerada como a diferença entre as cargas de montante e jusante:
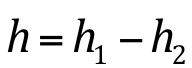
Bocais:
Os bocais ou tubos adicionais são constituídos por peças tubulares adaptadas aos orifícios. Servem para dirigir o jato. O seu comprimento deve estar compreendido entre 1,5 vezes e 3 vezes o seu diâmetro.
Bocais |
1,5 a 3 D |
Tubos muito curtos |
3 a 500 D |
Tubos curtos |
500 a 4000 D |
Tubos longos |
Acima de 4000 D |
Tabela 2: Classificação dos bocais:
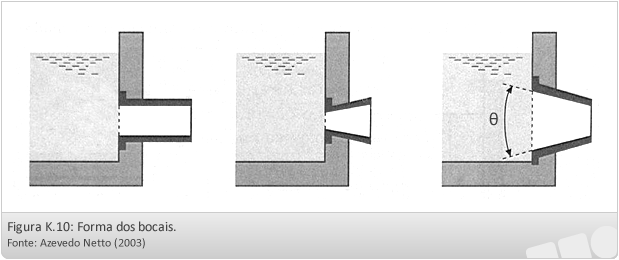
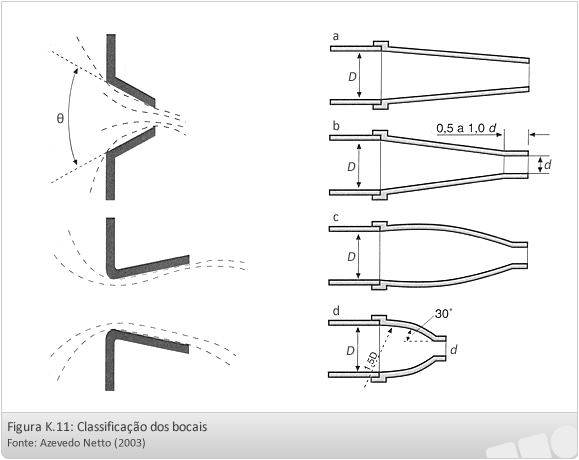
Os bocais costumam ser classificados em:
- Cilíndricos:
- interiores ou remanescentes (Cd = 0,51);
- exteriores (Cd = 0,82);
- Cônicos:
- Convergentes (Cd = 0,94);
- Divergentes (Cd = 0,97 a 0,98);
Na prática, os bocais são construídos para várias finalidades: combate a incêndios, operações de limpeza, serviços de construção, aplicações agrícolas, tratamento de água, máquinas hidráulicas, etc.
Cálculo da vazão nos bocais:
Aos bocais aplica-se a fórmula geral, deduzida para orifícios pequenos:
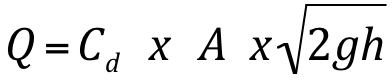
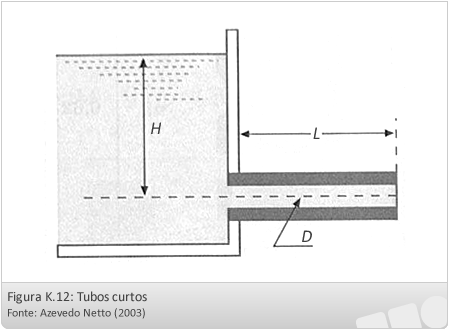
Tubos curtos:
Para citar exemplos mais comuns de tubos curtos, basta mencionar certos tipos de extravasores, canalizações para o esvaziamento de tanques, descarga de canalizações, bueiros, instalações industriais, etc.
Analisando-se os tubos curtos, sob um aspecto mais geral, encontra-se para L=0, orifícios; L=D, orifícios; L=2D, bocais; L=3D, bocais.
Quando o comprimento L ultrapassa em muitas vezes o diâmetro D, encontra-se o caso das tubulações:
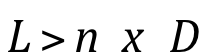
Teoricamente, o valor de n não deve ser inferior a 40 nos casos mais favoráveis, devendo exceder a 250, nos casos mais comuns. Merriman considerava o comprimento 500 x D como limite inferior para as tubulações propriamente ditas.
Cálculo de vazão em tubos curtos:
A determinação da vazão de tubos muito curtos sujeitos à descarga livre, pode ser feita aplicando-se a expressão geral de descarga nos bocais:
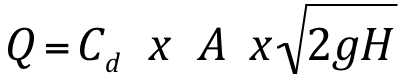
Onde:
Q – vazão (m3/s);
A – seção transversal de escoamento (área útil do tubo) (m2);
g – aceleração da gravidade (9,8 m/s2);
H – carga inicial disponível (m).
O coeficiente de descarga Cd (ou coeficiente de velocidade Cv) dependerá do comprimento relativo do tubo, isto é, de L/D:
Para orifícios em paredes delgadas:
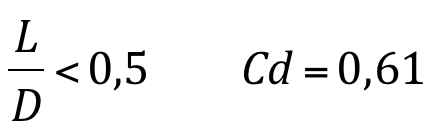
Para bocais, este valor se eleva:
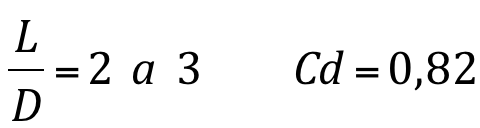
Para tubos muito curtos, o valor de Cd vai decrescendo, à medida que se eleva a relação L/D, em consequência da influência dos atritos internos e externos (parede do tubo).
Eytelwein obteve os seguintes resultados com tubos novos de ferro fundido, de 0,30m de diâmetro, ensaiados com uma carga inicial de 30 m.
|
Cd = 0,77 |
|
Cd = 0,73 |
|
Cd = 0,70 |
|
Cd = 0,66 |
|
Cd = 0,60 |
Vertedores:
Os vertedores podem ser definidos como simples paredes, diques ou aberturas sobre os quais um líquido escoa. O termo aplica-se, também, a obstáculos à passagem da corrente e aos extravasores.
Os vertedores são, por assim dizer, orifícios sem a borda superior.
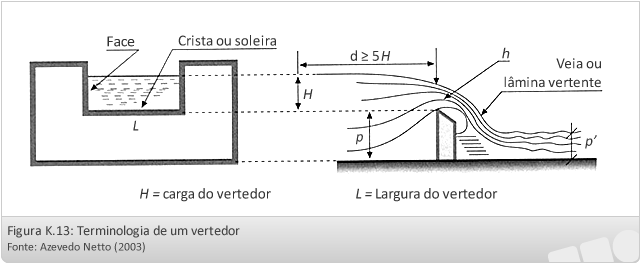
Classificação dos vertedores:
Forma:
- simples (retangular, trapezoidal, triangular, etc.)
- compostos (seções combinadas)
Altura relativa da soleira:
- Vertedores completos ou livres (p>p’)
- Vertedores incompletos ou afogados (p<p’)
Natureza da parede:
- vertedores em parede delgada (chapas ou madeira chanfrada)
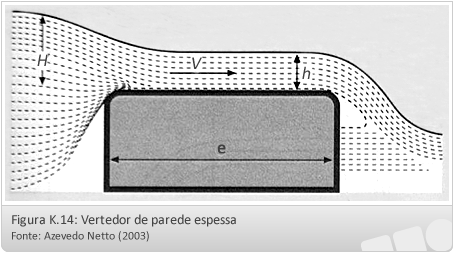
- vertedores em parede espessa (e > 0,66H)
Largura relativa:
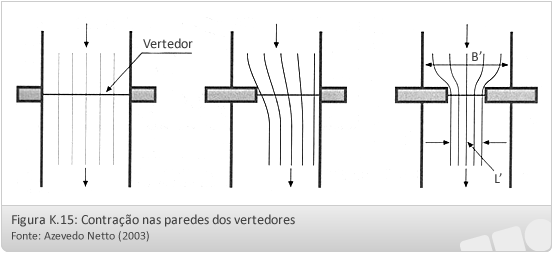
- vertedores sem contrações laterais (L = B)
- vertedores contraídos (L < B) (com uma contração ou com duas contrações)
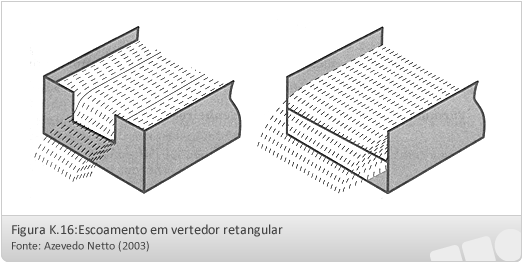
Vertedores retangulares de parede delgada:
Fórmulas práticas:
Fórmula de Francis:

Onde:
Q – vazão (m3/s)
L – comprimento de crista (m)
H – carga sobre o vertedor (m)
Influência das contrações:
As contrações ocorrem nos vertedores cuja largura é inferior a do canal em que se encontram instalados (L < B).
Deve-se considerar na aplicação da fórmula um valor corrigido para L:
- para uma contração:

- para duas contrações:

Vertedores trapezoidais ou de Cipolletti
Cipolletti procurou determinar um vertedor trapezoidal que compensasse o decréscimo de vazão devido às contrações.
A inclinação das faces foi estabelecida de modo que a descarga através das partes triangulares do vertedor correspondesse aos decréscimos de descarga, devido às contrações laterais, com a vantagem de evitar a correção nos cálculos.
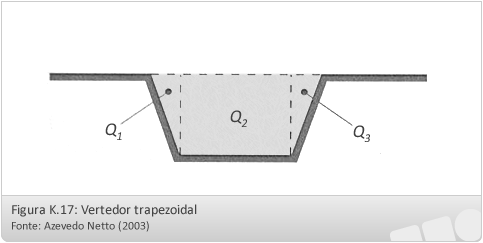
Para o cálculo da vazão é utilizado a mesma equação de Francis, com a vantagem de não ser necessário a correção das contrações:
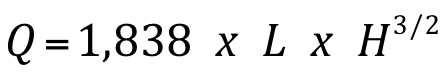
Vertedores Triangulares:
Os vertedores triangulares possibilitam maior precisão na medida de cargas correspondentes a vazões reduzidas. São geralmente trabalhados em chapas metálicas. Na prática, somente são empregados os que têm forma isósceles, sendo mais usual os de 900.
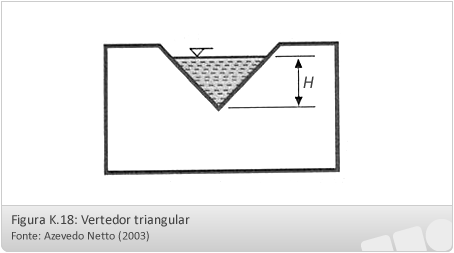
Para estes vertedores adota-se a fórmula de Thompson:
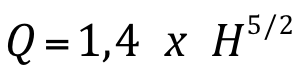
Onde:
Q – vazão (m3/s);
H – carga sobre o vertedor (m).
Vertedor Circular:
O vertedor de seção circular, embora raramente empregado, oferece como vantagem a facilidade de execução e não requer nivelamento da soleira.
A equação da vazão para um vertedor circular é a seguinte:
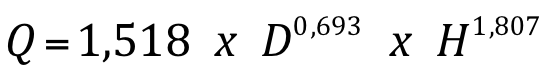
Onde:
Q – vazão (m3/s)
D – diâmetro do orifício (m)
H – carga sobre o vertedor (m)
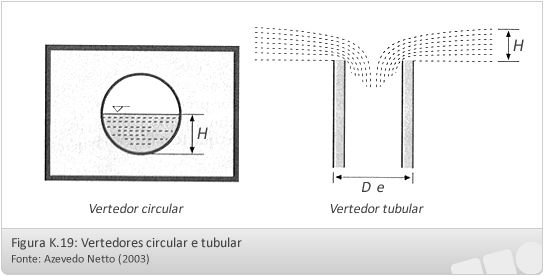
Vertedor Tubular:
Os tubos verticais instalados em tanques, reservatórios, caixas de água, etc, podem funcionar como vertedores de soleiras curvas, desde que a carga seja inferior à quinta parte do diâmetro externo (De):
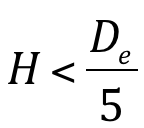
Para calcular a vazão aplica-se a seguinte equação:
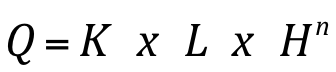
Onde:
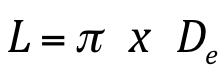
Valores de De (m) |
K |
0,175 |
1,435 |
0,25 |
1,440 |
0,35 |
1,455 |
0,50 |
1,465 |
0,70 |
1,515 |
Tabela 3: As experiências mostram que n = 1,42 e que o coeficiente K depende do diâmetro do tubo:
Vertedores de parede espessa:
Um vertedor é considerado de parede espessa, quando a soleira é suficientemente espessa para que na veia aderente se estabeleça o paralelismo dos filetes:
Aplicando-se Torricelli:
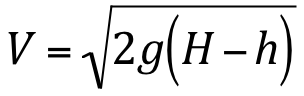
E
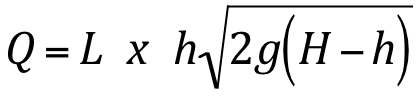
Ou para a largura unitária , L = 1:
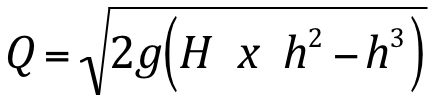
OU
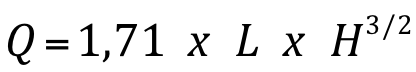
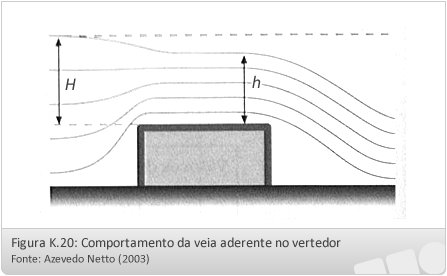
Medidor de regime crítico ou Parshall
Os medidores de regime crítico podem constituir num simples estrangulamento adequado de seção, no rebaixamento ou na elevação do fundo, ou ainda numa combinação conveniente dessas singularidades, capaz de ocasionar regime livre de escoamento.
Há uma grande variedade de medidores desse tipo, sendo bastante conhecidos os medidores Parshall.
Os medidores Parshall são constituídos por uma seção convergente, uma seção estrangulada e uma seção divergente.
Os medidores Parshall são muito indicados para medida de vazão de esgotos, pelo fato de não apresentarem arestas vivas ou obstáculos à corrente líquida.
Como a perda de carga é relativamente pequena, o seu emprego tende a se generalizar.
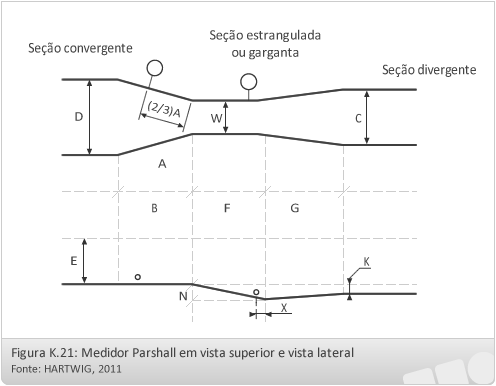
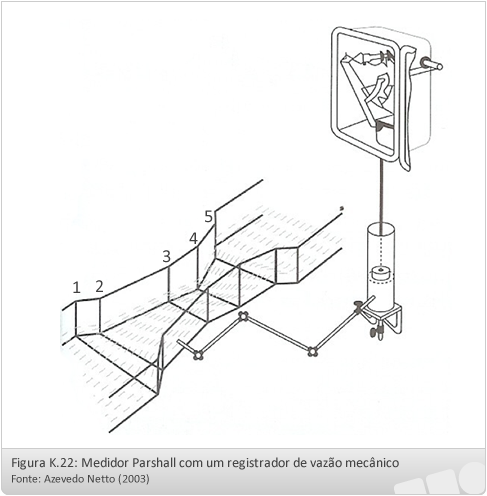
Classificação:
São indicados nominalmente pela largura da seção estrangulada.
-Na primeira seção (convergente) o fundo é em nível;
-Inclinado na garganta (9 vert; 24 horiz);
-Na seção divergente é em aclive (1 vert; 6 horiz).
Emprego
Regular a distribuição de água em propriedades agrícolas
Canais de rega, através de medidas de vazão
Medidas de vazão em estações de tratamento de água
Estações de tratamento de esgoto
Condições de descarga
a) Escoamento ou descarga livre
b) Afogamento ou submersão
No primeiro (a) se faz livre como nos vertedores, a veia líquida independe da condição de jusante, basta medir a carga Ha;
No segundo caso o nível da água a jusante é suficientemente elevado para influenciar e retardar o escoamento (descarga submersa);
-Causado por condições de jusante
- Obstáculos existentes;
-Falta de declividade nos trechos subsequentes.
Para medir a vazão é necessário medir uma segunda carga Hb próximo ao final da garganta
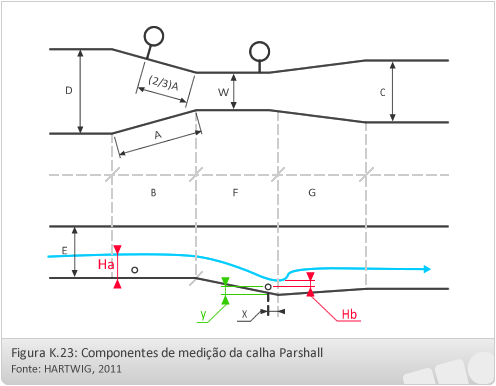
Se as leituras estiverem abaixo destes limites o escoamento será livre.
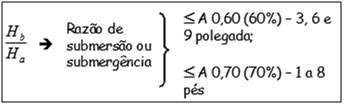
Vantagens dos medidores Parshall:
a)Facilidade de realização;
b)Baixo custo;
c)Não forma depósitos de material em suspensão;
d)Uma só medição de H é suficiente;
e)Os tamanhos mais variados já foram ensaiados, sem a necessidade de novos cálculos;
f)Emprega-se diversos materiais (alvenaria, concreto, madeira, metal, etc).
Locação dos medidores:
-Deve-se evitar grandes turbulências na sua seção inicial;
-Não devem ser instalados logo após uma comporta;
-Não devem ser instalados após uma curva.
Os turbilhonamentos poderiam provocar ondas ou sobreelevações capazes de comprometer a precisão dos resultados.
Fórmula geral para vazão:
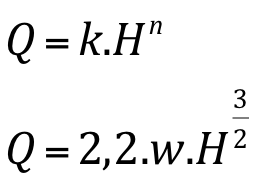
Onde:
K e n são tabelados;
W =tamanho do medidor (m);
Q = vazão (m3/s).
Escolha do medidor Parshall é função da:
Largura do canal existente;
-profundidade da água neste canal;
-perda de carga admissível;
-possibilidade de vazões futuras diferentes.
Existem tabelas com tamanhos de medidores levando em conta estes fatores, em regime de escoamento livre.
Extravasor de barragens
No traçado da seção transversal dos extravasores ou sangradouros das represas, ou no estudo do perfil das próprias barragens que funcionam afogadas, procura-se adotar a forma mais satisfatória, tendo-se em vista o escoamento da lâmina vertente.
A forma ideal é aquela que favorece a vazão ou descarga e que ao mesmo tempo, impede a ocorrência de efeitos nocivos à estrutura, tais como o vácuo parcial, as pulsações da veia, as vibrações, etc.
O traçado da crista deve ser feito para a vazão máxima esperada, isto é, para a maior carga admissível.
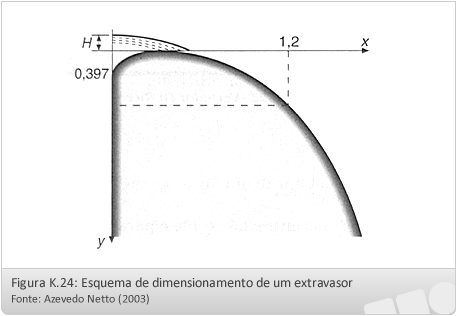
Tabela - perfil creager |
|||||
x |
y |
x |
y |
x |
y |
0,0 |
0,126 |
0,6 |
0,060 |
1,7 |
0,870 |
0,1 |
0,036 |
0,8 |
0,142 |
2,0 |
1,220 |
0,2 |
0,007 |
1,0 |
0,257 |
2,5 |
1,960 |
0,3 |
0,000 |
1,2 |
0,397 |
3,0 |
2,820 |
0,4 |
0,007 |
1,4 |
0,565 |
3,5 |
3,820 |
De acordo com as experiências de Creaguer e Escande, podem ser adotados os valores da tabela acima para uma carga H = 1,0 m. Para outros valores de H, basta multiplicar as coordenadas indicadas pelos mesmos. Nas condições ideais de projeto, pode-se aplicar a seguinte equação: